[자료구조] 트리 구조

트리의 개념

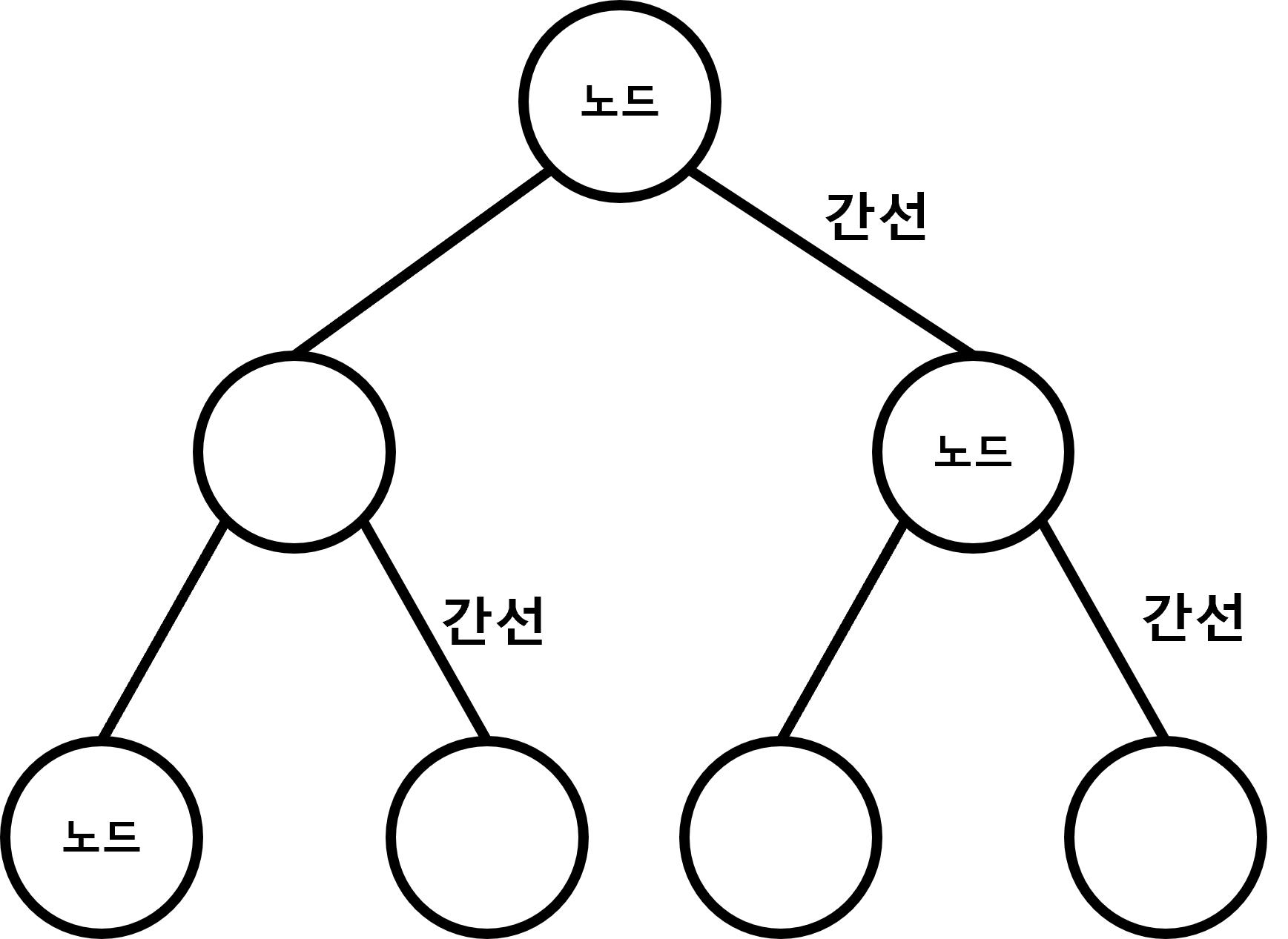
트리는 주요 자료구조 중 하나로 노드(Node)와 간선(Edge)들이 연결된 계층적 자료구조 입니다.
트리는 다양한 응용 분야에서 활용되며 특히, 계층적으로 데이터를 다루거나
데이터를 효율적으로 검색, 삽입, 삭제하는 작업에서 자주 사용됩니다.

단어 정리

기본

용어	설명
노드(Node)	트리에서 데이터(자식 노드, 값)를 저장하는 기본 요소
간선(Edge)	노드와 노드를 연결하는 선

노드 관계

용어	설명
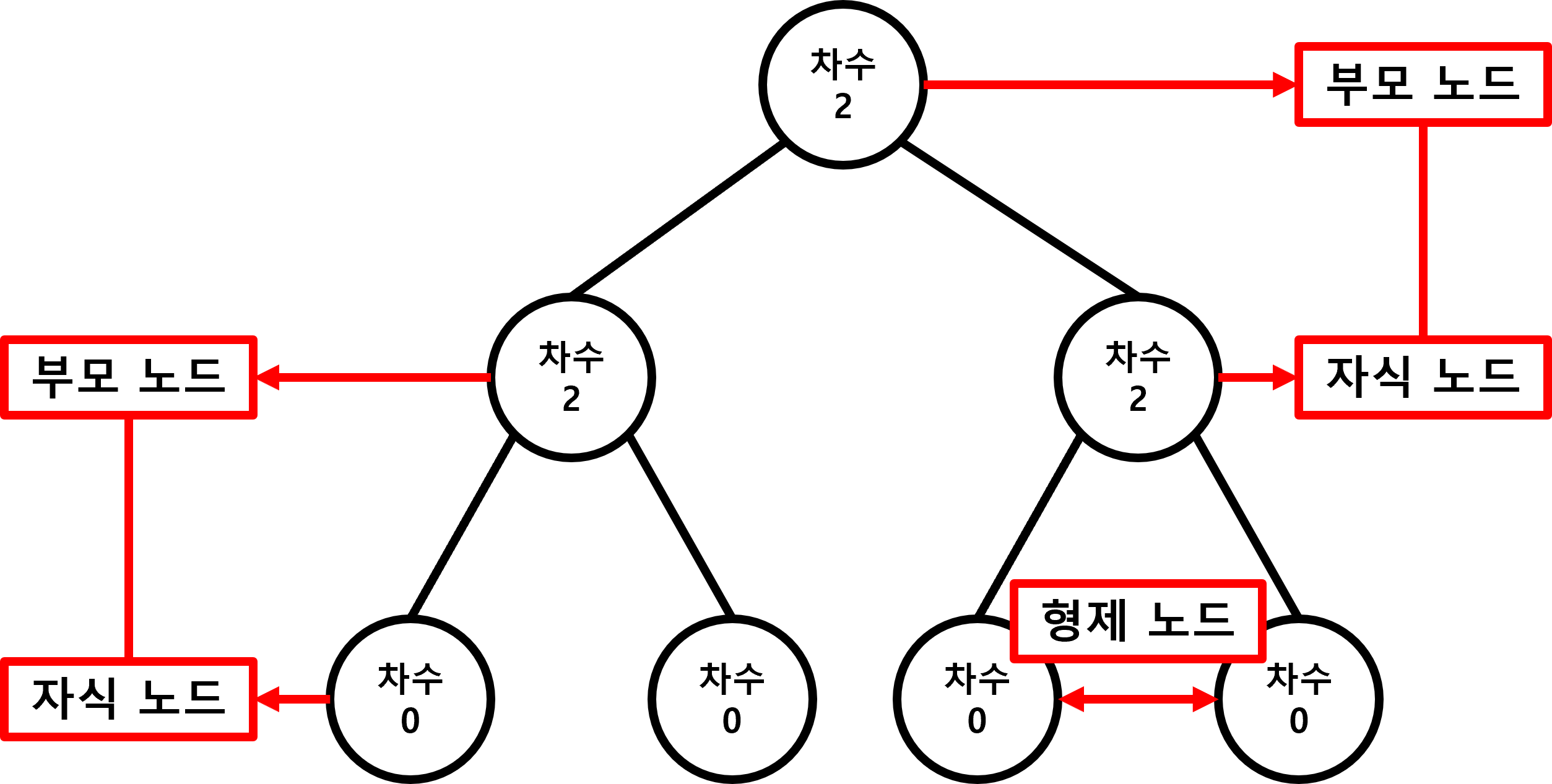
부모(Parent)	특정 노드의 바로 윗 단계에 위치하는 노드
자식(Child)	특정 노드의 바로 아랫 단계에 위치하는 노드
차수(Degree)	각 노드가 갖는 자식의 수 모든 노드의 차수가 N개 이하면 N진 트리라고 합니다.
형제(Sibling)	동일한 부모 노드를 갖는 노드
조상(Ancestor)	특정 노드에서 위쪽 간선을 따라 만나는 모든 노드
자손(Descendant)	특정 노드에서 아래쪽 간선을 따라 만나는 모든 노드

노드 역할

용어	설명
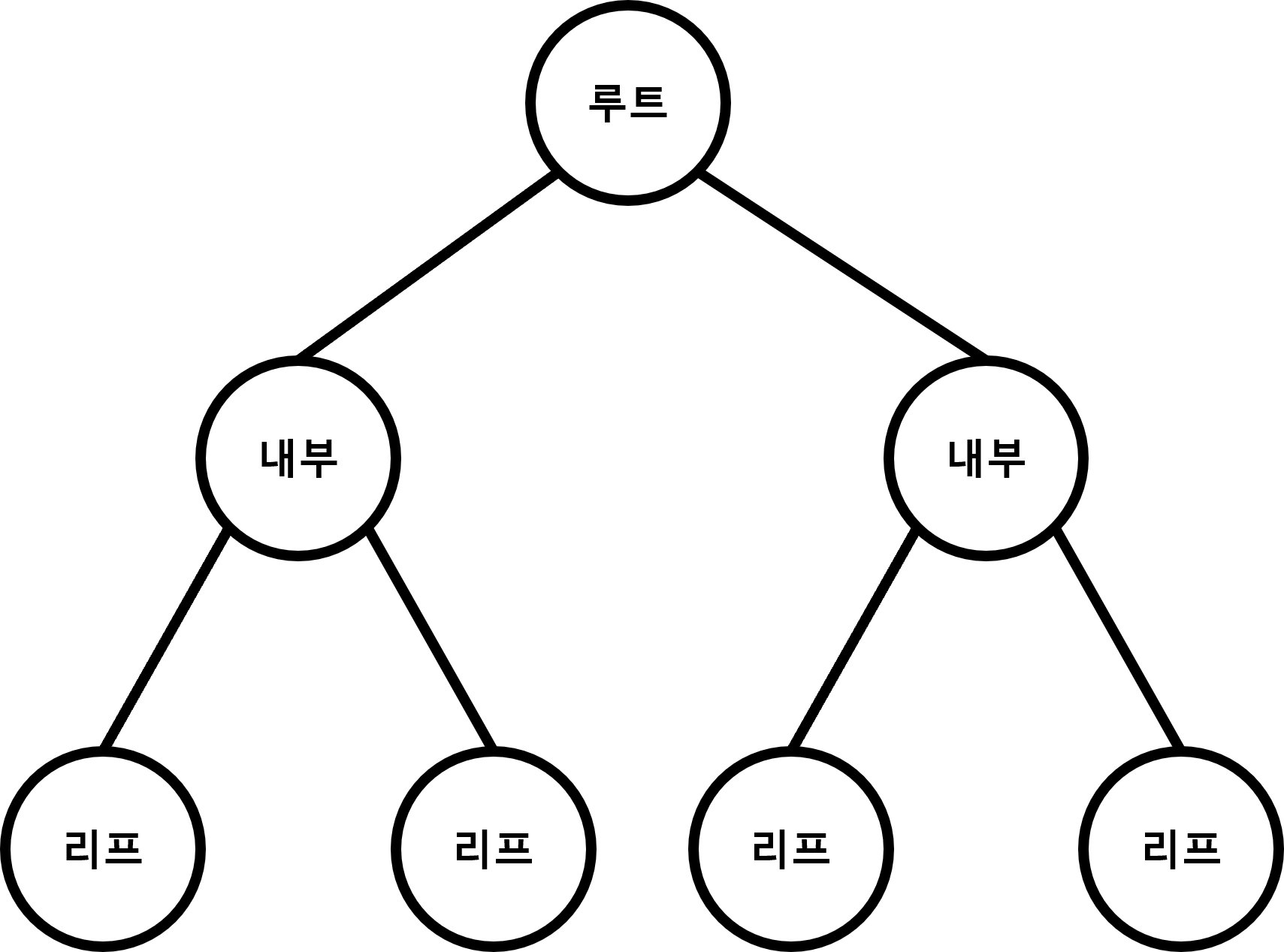
루트(Root) 노드	트리의 최상위에 위치하는 노드 트리에서 1개만 존재합니다.
리프(Leaf) 노드	자식이 없는 노드
내부(Internal) 노드	루트 노드와 리프 노드를 제외한 모든 노드

트리 구조

용어	설명
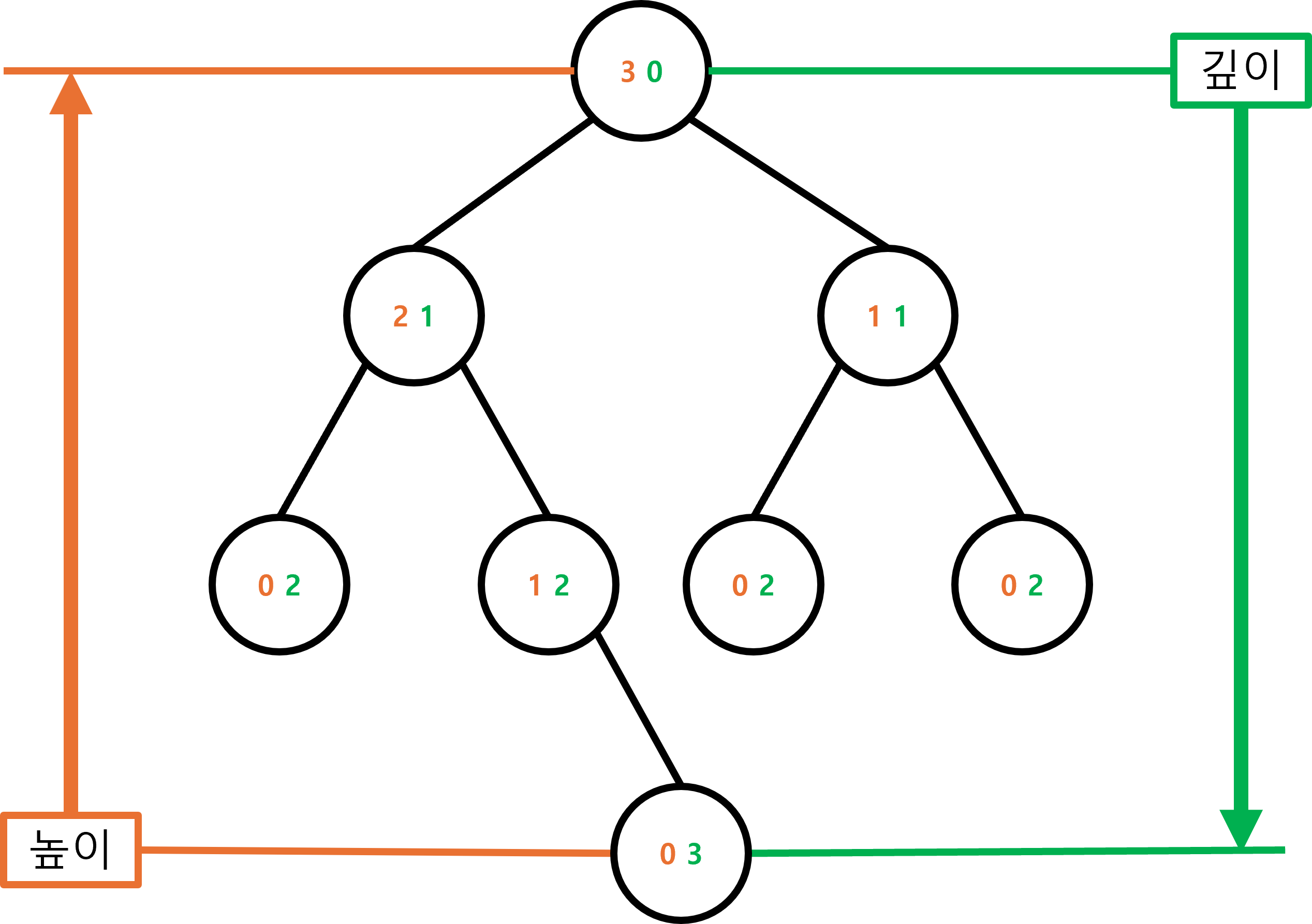
깊이(Depth)	루트 노드부터 특정 노드까지의 길이 루트 노드의 깊이는 0
노드 높이(Height)	특정 노드부터 아래로 연결된 가장 깊은 노드까지의 길이
트리 높이(Height)	루트 노드의 높이 값
서브(Sub) 트리	트리 전체가 아닌 일부분의 트리를 서브 트리라고 합니다. 이때, 서브 트리의 노드는 트리처럼 모든 노드가 간선으로 연결되어 있어야합니다.

트리의 특징

• 비선형 구조 : 한 노드가 여러 자식 노드와 연결되어 계층적 관계를 표현하는데 적합
• 비순환 구조 : 2개의 노드가 서로 부모이며 자식일 순 없기에 비순환 구조입니다.
• 하나의 루트 노드 : 모든 트리에서는 반드시 하나의 루트 노드만 존재해야 합니다.
• 하나의 경로 : 모든 노드는 루트 노드까지의 경로가 하나만 존재해야 합니다.

트리의 순회

트리의 모든 노드를 확인하는 방법은 전위 순회, 중위 순회, 후위 순회 로 3가지가 존재합니다.

전위 순회(Postorder)

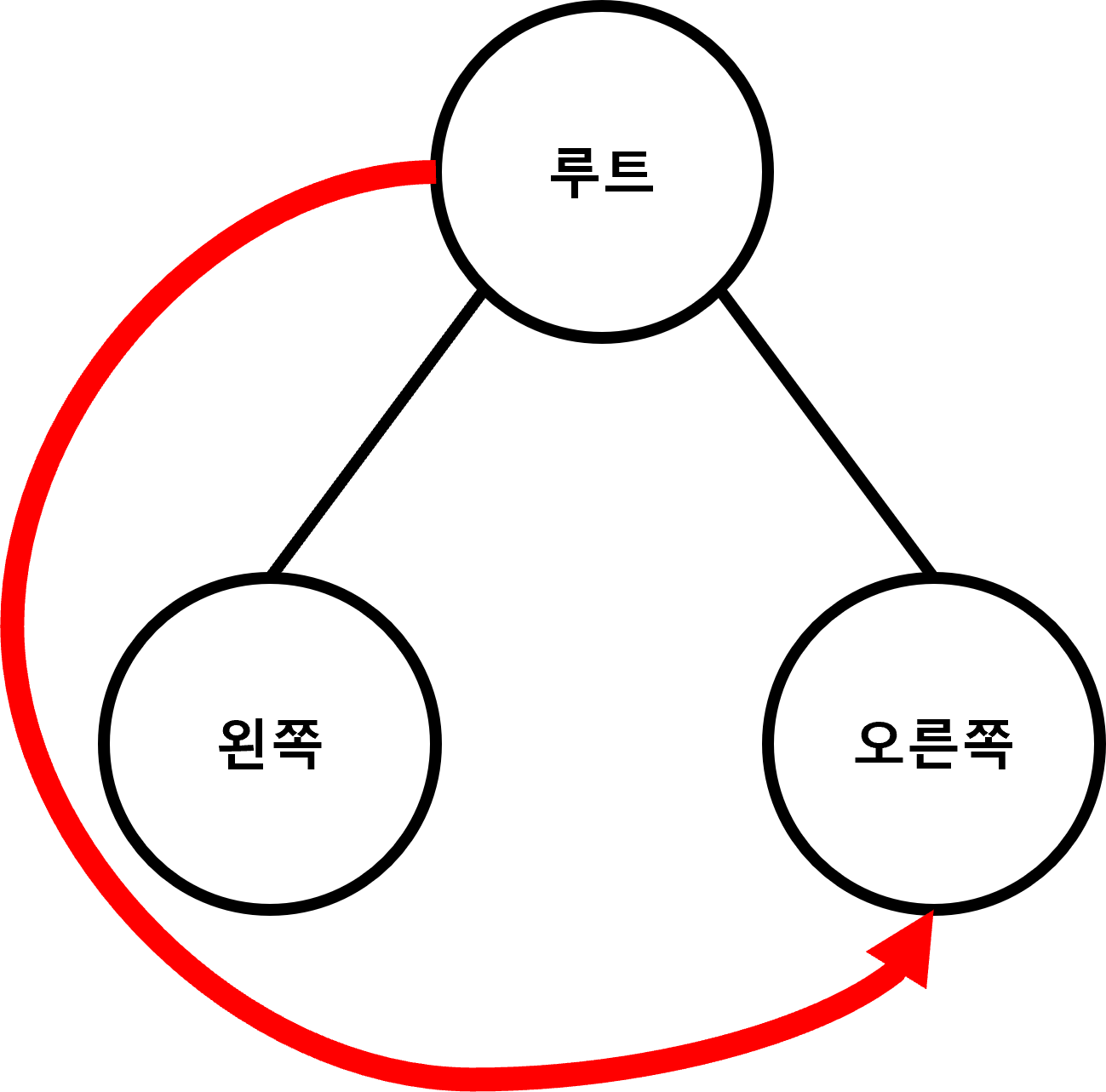
전위 순회는 노드들을 반시계 방향으로 순회하는 방법으로
루트 노드 -> 왼쪽 서브 트리 -> 오른쪽 서브 트리 순서로 노드를 방문합니다.

중위 순회(Inorder)

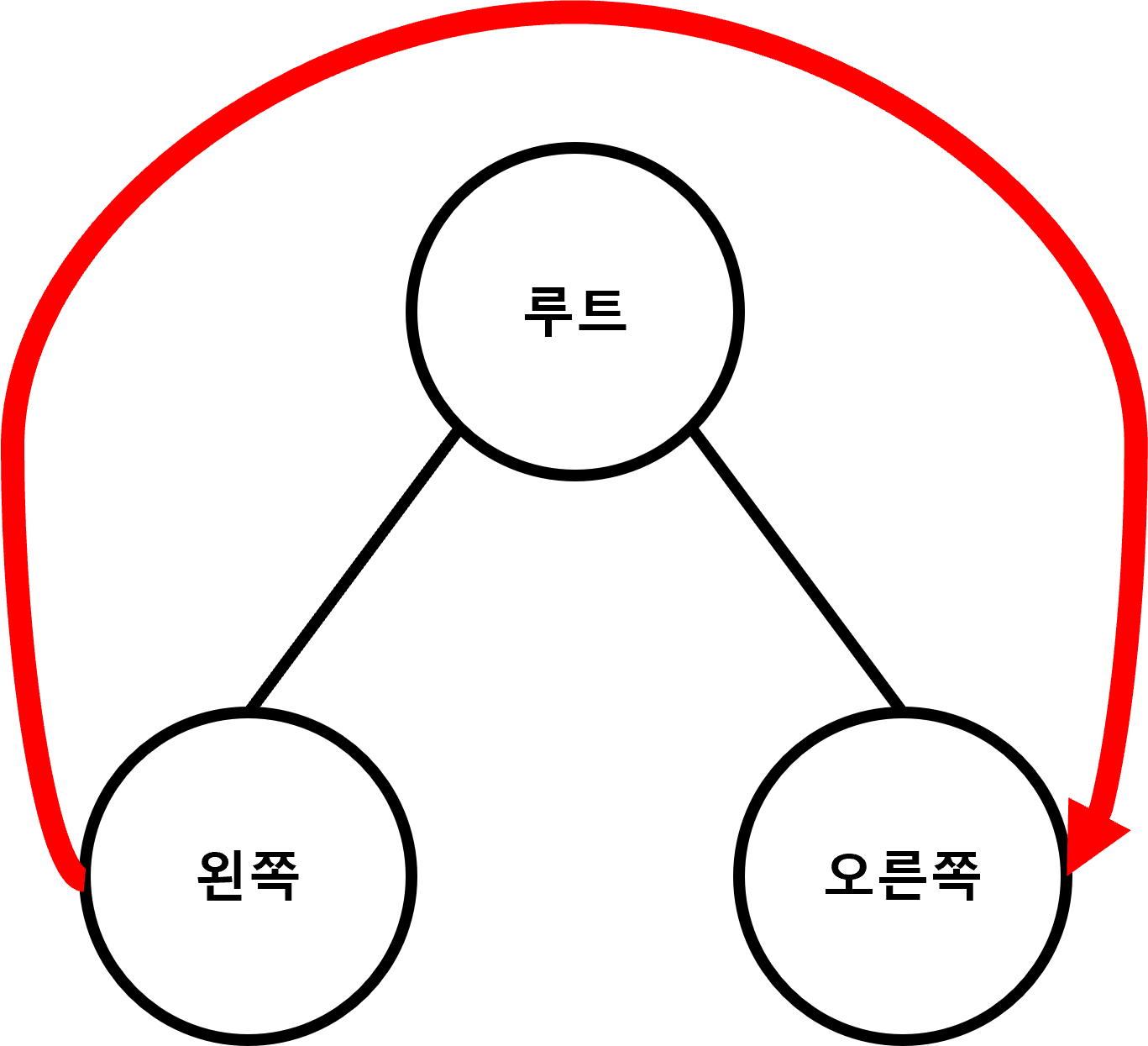
중위 순회는 노드들을 시계 방향으로 순회하는 방법으로
왼쪽 서브 트리 -> 루트 노드 -> 오른쪽 서브 트리 순서로 노드를 방문합니다.
만약 정렬된 이진 트리(이진 검색 트리)에서 중위 순회로 각 데이터를 출력할 경우
오름차순으로 데이터를 방문할 수 있습니다.

후위 순회(Inorder)

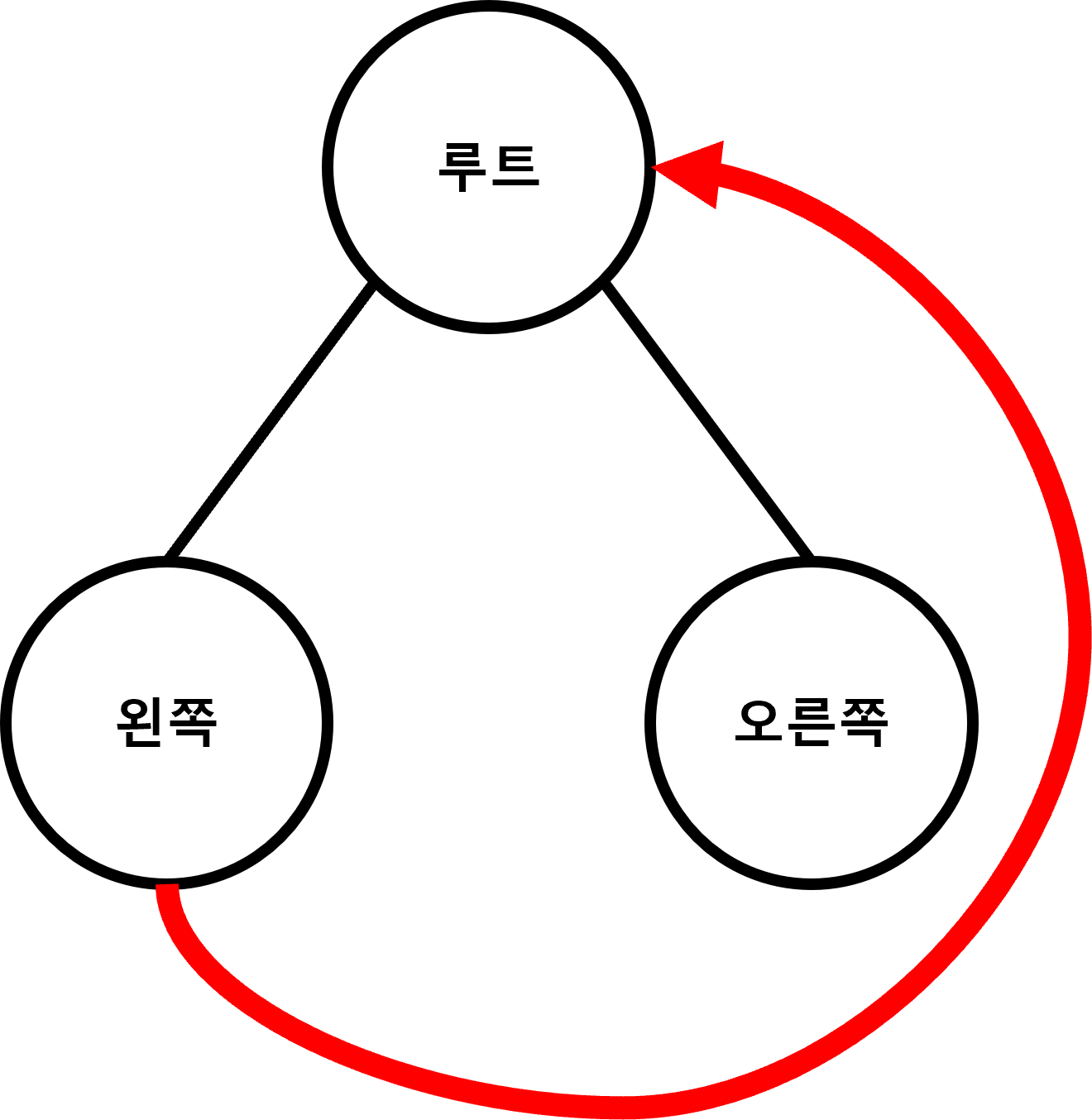
후위 순회는 전위 순회처럼 노드들을 반시계 방향으로 순회하는 방법이지만 순서가 다릅니다.
왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 루트 노드 순서로 노드를 방문합니다.

코드로 순회 만들기

C++ 를 이용해서 전위, 중위, 후위 순회로 트리를 순회하여
각 노드에 있는 데이터를 순서대로 출력해 보았습니다.

// 노드 구조체
struct NODE {
    char data;
    NODE* left;
    NODE* right;
};

// 전위 순회
void preorder(NODE* curr) {
    if(curr != nullptr) {
        printf("%c", curr->data);   // 데이터 출력
        preorder(curr->left);
        preorder(curr->right);
    }
}

// 중위 순회
void inorder(NODE* curr) {
    if(curr != nullptr) {
        inorder(curr->left);
        printf("%c", curr->data);   // 데이터 출력
        inorder(curr->right);
    }
}

// 후위 순회
void postorder(NODE* curr) {
    if(curr != nullptr) {
        postorder(curr->left);
        postorder(curr->right);
        printf("%c", curr->data);   // 데이터 출력
    }
}

참고한 백준 문제