[Algorithm] Rabin-karp 알고리즘
이전 문자열 매칭 포스트인 KMP 알고리즘 O(M + N)과 동일하게 특정 문자열을 찾고자 할 때 사용되는 알고리즘인
라빈카프 알고리즘을 이번 포스트에서 설명해보겠습니다.
라빈카프 알고리즘에서 해싱(Hashing) 사용 방법
라빈카프 알고리즘은 해싱으로 문자열을 탐색하는 알고리즘입니다.
문자열 M에서 문자열 N을 찾는 상황에서 라빈카프 알고리즘을 설명해보겠습니다.
라빈카프의 순서는 다음과 같습니다.
- 문자열 N 의 해시값을 저장합니다.
- 문자열 M 에서 문자열 N 길이만큼 해시값을 구해 문자열 N의 해시값과 비교합니다.
- 비교한 값이 같을 경우, 문자를 한 개씩 비교합니다.
- 비교한 값이 다를 경우, 문자열 N 을 한 칸 이동해 새로운 해시값과 비교합니다.
이때, 해싱을 사용함에도 불구하고 2-1 과정에서 문자를 한 개씩 비교하는 이유는
입력 값이 다른 해시 함수에서 같은 해시값이 나오는 해시 충돌(Hash Collision) 을
방지하고자 한 것 입니다.
해싱을 이용한 탐색 방법
문자열의 해시값이 다를 때 마다 한 칸씩 이동하면서 매번 새롭게 해시값을 구하는 것은
해시값을 이용해 성능향상을 시키고자한 목표에 방해가 됩니다.
따라서 이 문제점을 개선하기 위해 사용되는 것이 Rolling Hash 입니다.
Rolling Hash 는 매번 새롭게 해시값을 계산하는 것이 아닌 이전 값을 활용해 다음 값을 구하는
Hash Function 입니다.
문자열 M 에서 구한 해시값이 문자열 N 의 해시값과 달라 한 칸 이동한 뒤
1. 왼쪽에서 제거된 해시값을 기존 해시값에서 빼고
2. 중간 부분의 해시값을 재계산한 뒤
3. 오른쪽에서 추가된 해시값을 추가하면
새롭게 해시값을 구할 때 보다 비교적 적은 연산으로 다음 해시값을 구할 수 있습니다.
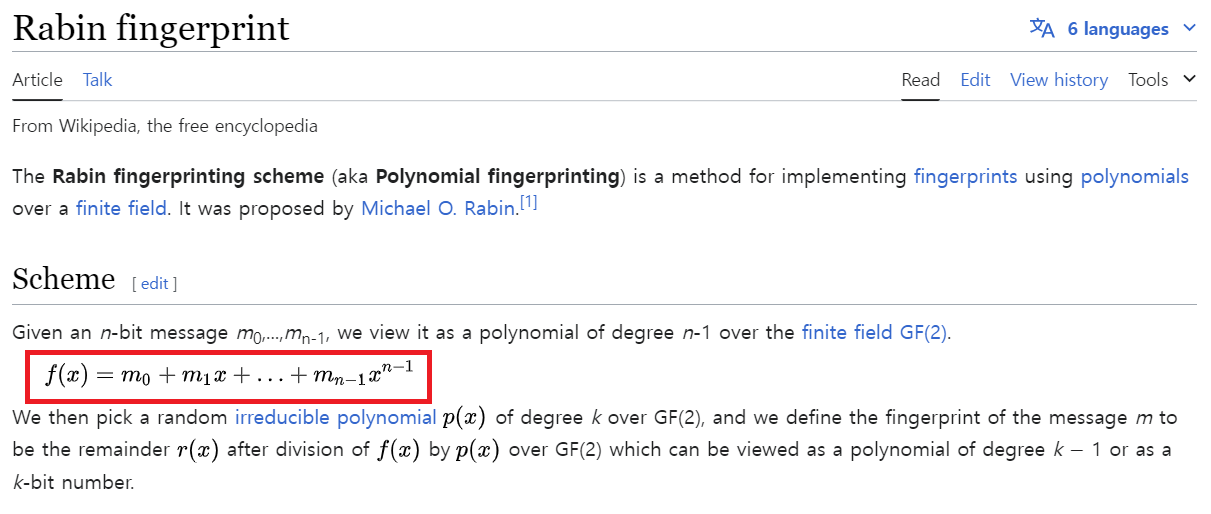
2번에서 설명한 중간 부분 재계산은 Rabin fingerprint라는 함수로 계산합니다.
이 함수에서 m은 문자열의 각 자리에 해당하는 문자이며 값은 보통 아스키 코드를 사요합니다.
각 자리 옆에 곱해지는 x의 값은 무엇이든 상관없지만 보통 2 를 사용합니다.
예를들어, “abc” 라는 문자열의 해시값을 구하면 다음과 같습니다.
“abca”에서 “abc”의 다음 문자열인 “bca” 의 해시값은 위의 처럼 새롭게 구하는 것이 아닌
이전 값을 빼고, 중간값을 재계산한 뒤 새로운 값을 더해 구합니다.
따라서 689에서 “a”의 해시값인 \(97 \times 2^2 = 388\) 을 683에서 뺀 값인 295에서
이전 해시함수에서 자리 수 마다 2의 제곱근을 해줬으므로 295에 2를 곱해 590을 저장합니다.
그리고 오른쪽에 새롭게 추가된 “a”의 해시값 \(97 \times 2^0 = 97\) 을 더해서
687 이라는 새로운 해시값이 나오게 됩니다.
따라서 찾고자 하는 해시값이 나올 때 까지 위의 과정을 반복하고
해시값을 찾았을 때, 문자열을 비교함으로서 해시충돌로 인한 잘못된 출력을 막을 수 있습니다.
구현 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// ws : 검색 대상 문자열 , ps : 검색할 패턴 문자열
void rabin_karp(string str, string target)
{
int strSize = str.size();
int targetSize = target.size();
int strHash = 0, targetHash = 0;
int power = 1;
for (int i = 0; i <= strSize - targetSize; ++i)
{
if (i == 0)
{
for (int j = 0; j < strSize; ++j)
{
strHash += (str[strSize - 1 - j] * power);
targetHash += (target[strSize - 1 - j] * power);
if (j < strSize - 1)
{
power *= 3;
}
}
}
else
{
strHash = 3 * (strHash - str[i - 1] * power)
+ str[targetSize - 1 + i];
}
if (strHash == targetHash)
{
for (int j = 0; j < targetSize; ++j)
{
if (str[i + j] != target[j])
{
cout << strHash << " " << targetHash << endl;
printf("%d\n", i + 1);
break;
}
}
}
}
}