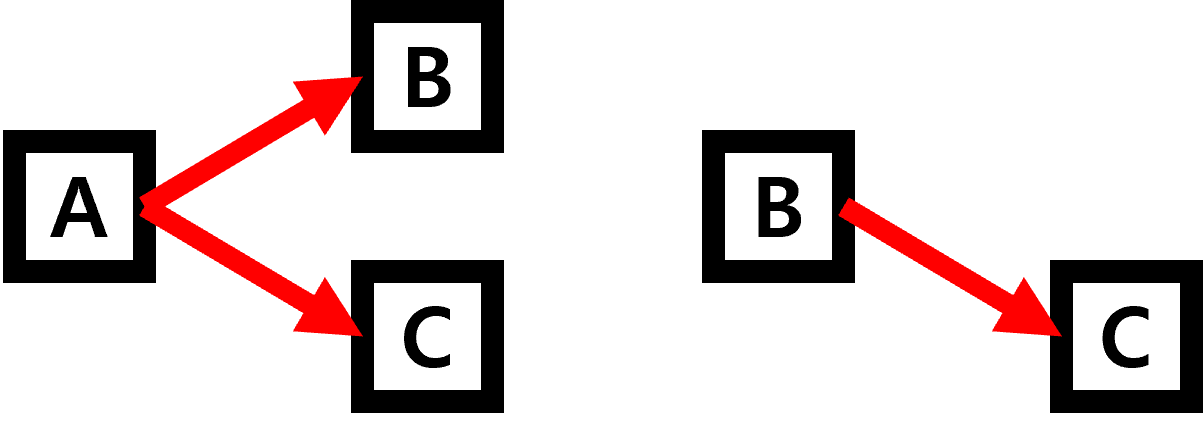[Math] 순열과 조합
일상 생활 속 경우의 수는 다양한 곳에서 확인할 수 있습니다.
예를들어, 아이스크림 가게에서 아이스크림 맛을 r개 선택할때,
중복을 허용해 같은 맛을 여러 개 선택할 지, 컵에 쌓을 때, 순서는 어떻게 할지 등 여러 경우의 수가 존재합니다.
이러한 경우의 수가 몇 개 존재하는지 확인할 수 있는 방법이 순열과 조합입니다.
순열과 조합은 n개의 원소에서 r개의 원소를 선택한다는 과정은 같지만
중간에 들어가는 조건이 다릅니다.
먼저, 순열의 경우 n개의 원소에서 r개의 원소를 선택할 때,
중복 없이, 순서를 고려해서 경우의 수를 확인합니다.
반면, 조합의 경우 중복 없이, 순서를 고려하지 않고 경우의 수를 확인합니다.
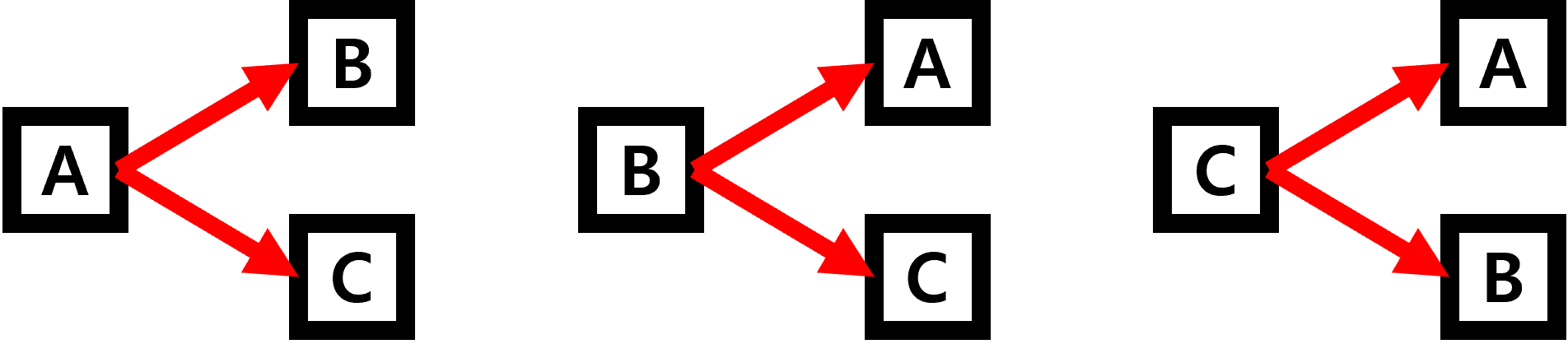
3개의 원소 중 2개의 원소를 선택하는 순열의 경우의 수는 무엇이 있는지 확인해 보겠습니다.
순열의 조건은 중복 없이 순서를 고려해서 선택하는 경우의 수 입니다.
따라서 위 그림에서 선택된 (A, B)와 (B, A)는 선택된 순서가 다르므로 다른 경우의 수 입니다.
그림에서 확인할 수 있듯이 총 경우의 수는 6개로
(A, B), (A, C), (B, A), (B, C), (C, A), (C, B) 가 있습니다.
순열의 표기 방법은 Permutation의 P를 사용해서 다음과 같이 표현합니다.
순열의 계산 방법은 n부터 r까지의 곱으로 아래와 같은 수식으로 계산됩니다.
이번에는 순열과 동일한 원소에서 조합의 경우의 수를 확인 해보겠습니다.
조합의 조건은 중복 없이, 순러를 고려하지 않고 선택하는 경우의 수 입니다.
따라서 순열과 달리 순서를 고려하지 않기 때문에 (A, B), (B, A)는 서로 같은 경우의 수가 됩니다.
그림에서 확인살 수 있듯이 총 경우의 수는 3개로
(A, B), (A, C), (B, C) 가 있습니다.
조합의 표기 방법은 Combination의 C를 사용해서 다음과 같이 표현합니다.
조합의 계산 방법은 n개의 원소에서 r개의 원소 선택인 순열 에서 중복을 제거하는 방법으로 진행됩니다.