[프로그래머스] 징검다리

이 포스트는 프로그래머스 사이트의 징검다리 문제 풀이입니다.

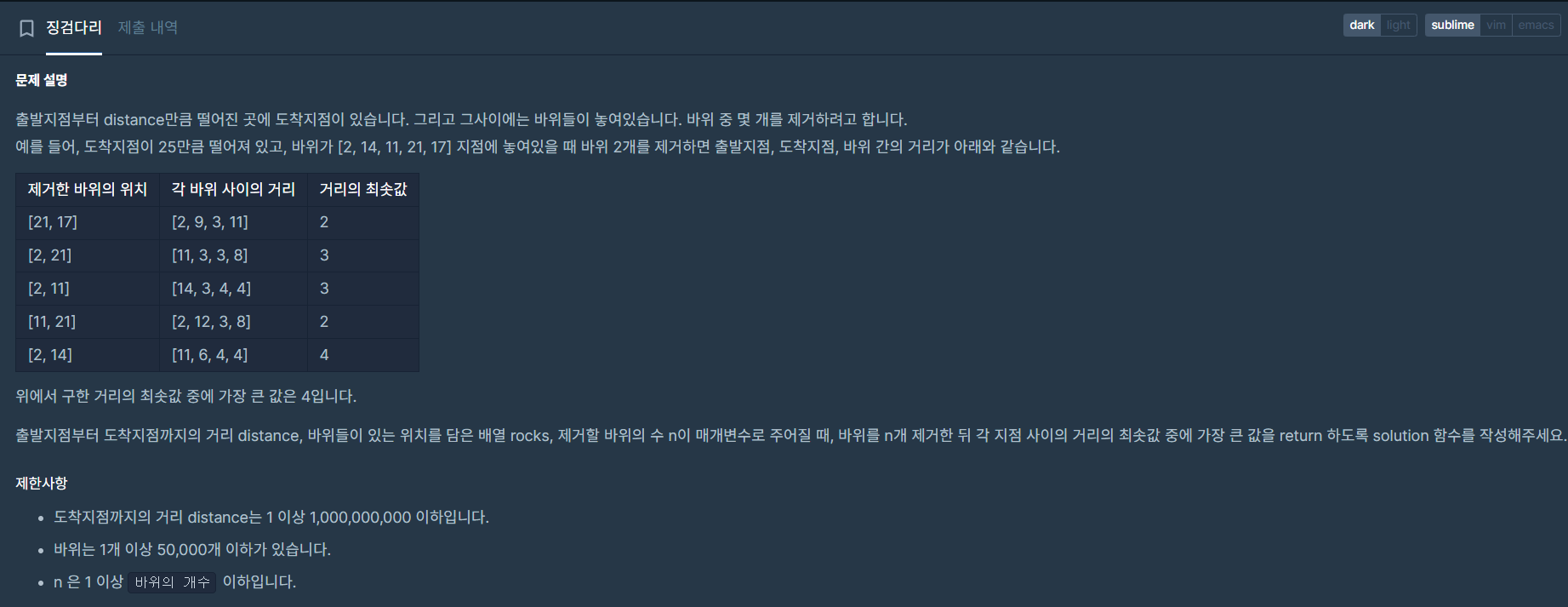
문제

해결 과정

이 문제는 rocks 배열에 저장된 위치에 distance 거리 안에 돌이 배치되어 있을 때, n개를 제거한 뒤
인접한 돌의 최소 거리 중 최댓값을 구하는 문제입니다.

처음 문제를 시도할 때, 저는 (rocks.size() - n)개의 돌을 선택하는 조합을 사용했습니다.
이 방법은 rocks 배열이 작거나 n이 작으면 문제를 해결할 수 있지만, 클 경우는 시간초과가 발생합니다.

첫 번째 시도 (실패)

#include <string>
#include <vector>
#include <algorithm>

#include <iostream>

using namespace std;

int solution(int distance, vector<int> rocks, int n) {
    sort(rocks.begin(), rocks.end());
    
    vector<bool> select(rocks.size(), true);
    for(int i = 0; i < n; ++i) {
        select[i] = false;
    }
    
    int MAX = 0;
    do {
        int MIN = 2e9;
        int prev = -1;
        for(int i = 0; i < rocks.size(); ++i) {
            if(select[i]) {
                if(prev != -1) {
                    MIN = min(MIN, rocks[i] - prev);
                } else if(prev == -1) {
                    MIN = min(MIN, rocks[i]);
                }
                prev = rocks[i];
            }
        }
        MIN = min(MIN, distance - prev);
        MAX = max(MIN, MAX);
    } while(next_permutation(select.begin(), select.end()));
    
    return MAX;
}

두 번째 시도 (성공)

그래서 두 번째 시도에서는 돌 중심의 거리 측정이 아니라
거리 중심의 돌 측정을 사용하였습니다.
문제의 답은 반드시 distance 보다 작으므로 distance 내부의 거리를 이분탐색하며
매번 삭제된 돌의 개수를 확인한 뒤 거리 범위를 줄이면서 이분탐색을 진행합니다.

#include <string>
#include <vector>
#include <algorithm>

#include <iostream>

using namespace std;

int get_remove_rock_cnt(vector<int>& rocks, int mid, int distance) {
    int prev = 0;
    int end = distance;
    
    int remove_cnt = 0;
    for(int rock : rocks) {
        if(rock - prev < mid) {
            remove_cnt++;
        } else {
            prev = rock;   
        }
    }
    
    return (end - prev < mid ? remove_cnt + 1 : remove_cnt);
}

int solution(int distance, vector<int> rocks, int n) {
    sort(rocks.begin(), rocks.end());
    
    int left = 1;
    int right = distance;
    int mid;
    
    int answer = 0;
    while(left <= right) {
        mid = (left + right) / 2;
        
        if(get_remove_rock_cnt(rocks, mid, distance) <= n) {
            answer = mid;
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return answer;
}

제출 결과