[자료구조] 그래프 자료구조의 기본
그래프는 다른 포스트에서 설명했던 트리처럼 노드와 간선을 사용하는 자료구조입니다.
그러나 트리와 전혀 다른 자료구조로 몇 가지 명확한 차이점이 존재합니다.
따라서 이번 포스트에서는 그래프가 무엇이고
그래프의 특징은 무엇이 있으며, 어디에서 사용하는지 알아보겠습니다.
그래프 (Graph)
그래프는 노드(Node, 혹은 버텍스(Vertex))와 간선(Edge)로 구성된 자료구조 입니다.
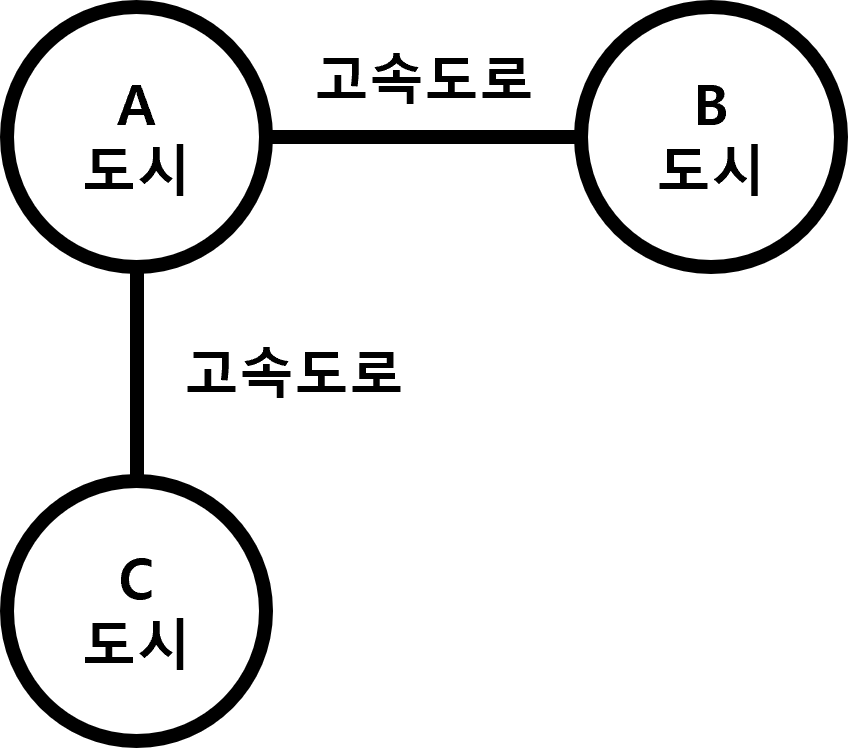
일반적으로 노드와 간선은 도시(노드)와 도시들을 잇는 도로(간선)으로 자주 표현됩니다.
그 외에도 지하철 노선도의 최단 경로, 도로 표시 등 연결되어 있는 객체 간 관계를 표현할 수 있습니다.
그래프의 특징
그래프는 트리와 몇 가지 동일한 용어를 사용하지만 의미가 다른 용어가 존재합니다.
| 용어 | 설명 |
|---|---|
| 노드(정점) | 그래프에서 출발, 경유, 도착이 될 수 있는 위치 |
| 간선 | 노드 간 관계를 표시하는 선 |
| 단방향(방향) | 한 방향으로만 이동 가능한 간선, 제시된 방향의 역방향은 이용 불가능 |
| 무방향(양방향) | 양방향 모두 이용 가능한 간선 |
| 가중치 | 특정 간선을 이용할 때, 필요한 비용 |
| 인접 노드 | 특정 노드에서 간선 1개로 연결된 또 다른 노드 |
| 정점 차수 | 무방향 그래프에서 하나의 정점에 인접한 정점의 수 |
| 진입 차수(내차수) | 방향 그래프에서 외부에서 들어노는 간선의 수 |
| 진출 차수(외차수) | 방향 그래프에서 외부로 나가는 간선의 수 |
| 경로 길이 | 출발 노드에서 도착 노드까지 경로를 구성하는데 사용된 간선의 수 |
| 사이클 | 경로의 시적 노드와 도착 노드가 동일할 때 |
그래프의 종류는 다음과 같습니다.
- 무방향(양방향) 그래프: 간선을 통해 양쪽 노드로 이동할 수 있는 그래프
- 방향(단방향) 그래프: 간선으로 한쪽 방향으로만 이동할 수 있는 그래프
- 가중치 그래프: 간선 이용시 비용이 들어가는 그래프
- 연결 그래프: 모든 노드가 연결되어 있는 그래프
- 비연결 그래프: 연결 그래프와 달리 한 정점에서 다른 정점까지 경로가 존재하지 않는 그래프
- 순환 그래프(사이클): 그래프에서 경로의 시작 노드와 도착 노드가 같은 그래프
- 비순환 그래프: 사이클이 존재하지 않는 그래프
- 완전 그래프: 그래프에 속해 있는 모든 정점이 서로 연결되어 있는 그래프
그래프 구현 방법
인접 리스트 (Adjacency List)
인접 리스트로 노드 간 관계를 표현하는 방법입니다.
그래프에 존재하는 모든 노드들이 각자 인접한 노드 리스트를 갖는 방법으로
위 도시 그래프를 인접 리스트로 표현하면 다음과 같습니다.
| 현재 도시(노드) | 인접 도시(노드) |
| A 도시 | B 도시, C 도시 |
| B 도시 | A 도시 |
| C 도시 | A 도시 |
현재 도시를 저장할 때는 배열 혹은 해시 테이블 을 사용하며
인접 도시를 저장할 때는 배열, 동적 리스트 등을 사용합니다.
인접 행렬 (Adjacency Matrix)
인접 행렬은 노드의 개수가 N 개일 때, N x N 행렬에서 노드 간 관계(간선)을 표시하는 방법입니다.
인접 행렬을 사용하면 간선의 수와 무관하게 \(N^2\) 의 메모리 공간이 필요합니다.
또한 인접한 노드를 확인하기 위해서는 N 개의 노드를 순회하며 간선 존재 여부를 확인해야 합니다.
그래프 탐색
그래프의 탐색은 너비 우선 탐색(BFS)와 깊이 우선 탐색(DFS)가 존재합니다.
자세한 내용은 다른 포스트에서 설명하겠습니다.
개인 공부 기록용 블로그입니다. 틀린 부분이 있을 경우 댓글 혹은 메일로 지적해주시면 감사하겠습니다!