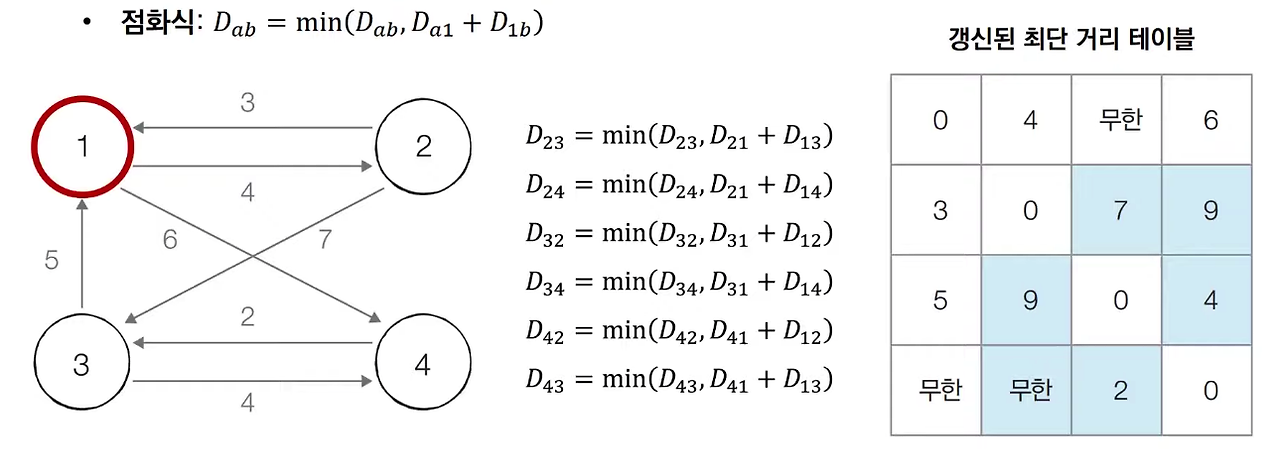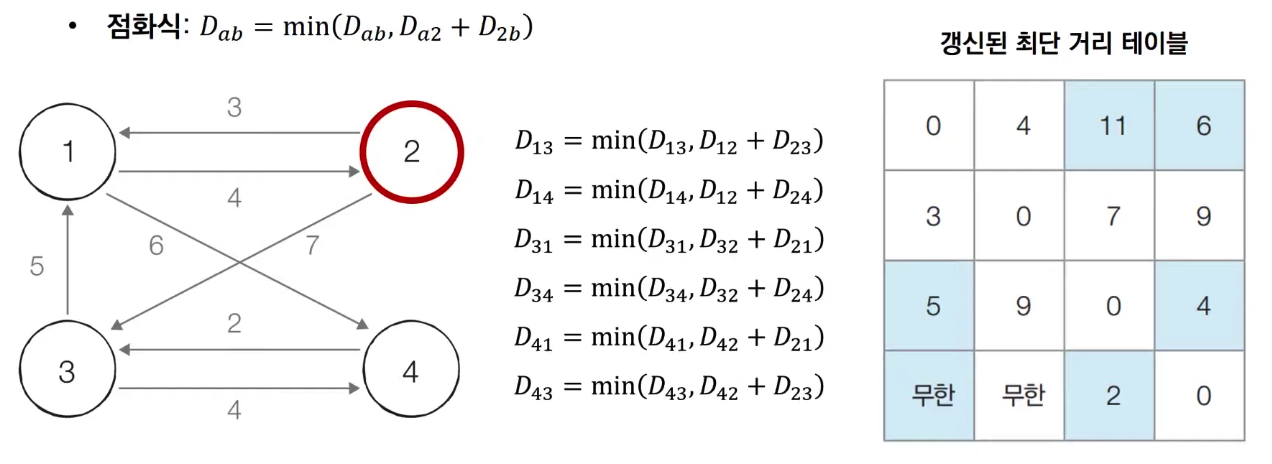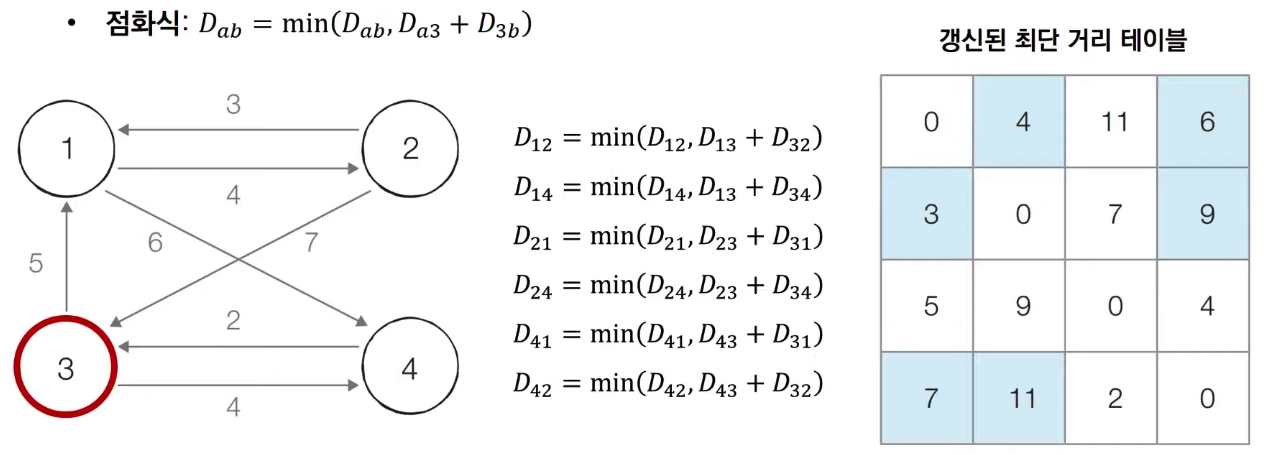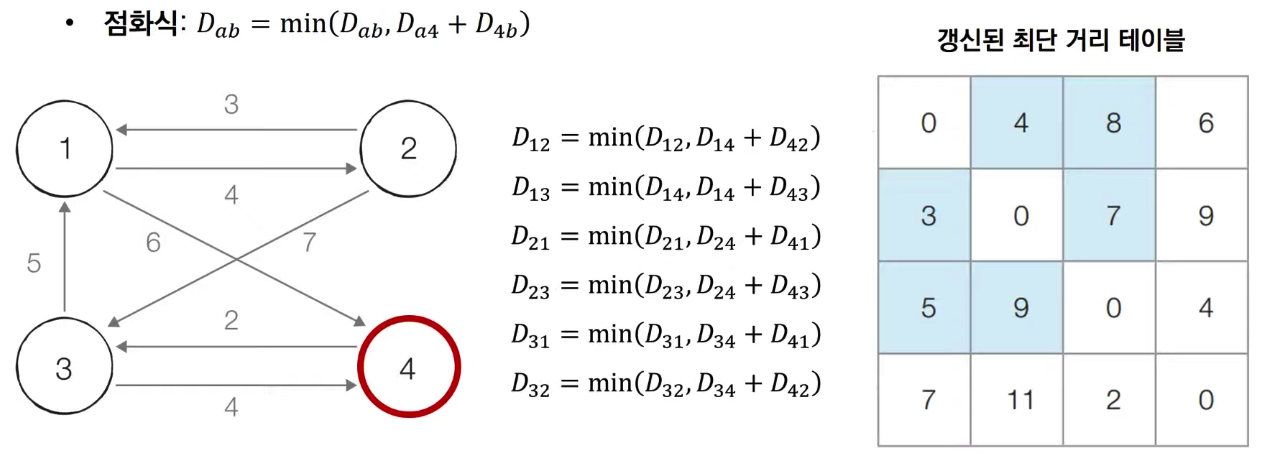[알고리즘] 플로이드 워셜(Floyd Warshall)

이것이 취업을 위한 코딩 테스트다 with 파이썬 (나동빈 저) 를 참고해 작성한 포스트입니다.

이전 포스트 에서 다익스트라 최단 경로 알고리즘에 대해서 설명했습니다.
다익스트라 알고리즘은 한 지점에서 다른 지점까지 의 최단 경로를 빠르게 구할 수 있는 알고리즘 이였습니다.
만약 그래프에 존재하는 N 개의 점이 서로의 최단 경로를 모두 알고 싶다면
각 노드에서 다른 노드까지의 모든 최단 경로를 N 번 반복해서 구하야 할까요?

모든 경로를 다익스트라 알고리즘으로 구할 수는 있지만
연산을 완료하는데 필요한 시간이 길 수 있습니다.
따라서 모든 지점에서 다른 모든 지점까지의 최단 경로 를 구하는 알고리즘인
플로이드 워셜 알고리즘을 사용하면 됩니다.

플로이드 워셜 알고리즘 특징

• 모든 지점에서 다른 모든 지점까지의 최단 경로 를 구해야할 때, 사용되는 알고리즘
• 그래프의 간선이 양방향, 단방향 모두 가능하며, 양방향에서 방향에 따라 가중치가 달라도 가능
• 최단 경로를 2차원 배열 에 저장
• 구현이 다익스트라 알고리즘 보다 쉽다.

다익스트라 알고리즘과 가장 큰 차이점은 2차원 배열 을 이용해 최단 경로를 갱신하는 것입니다.
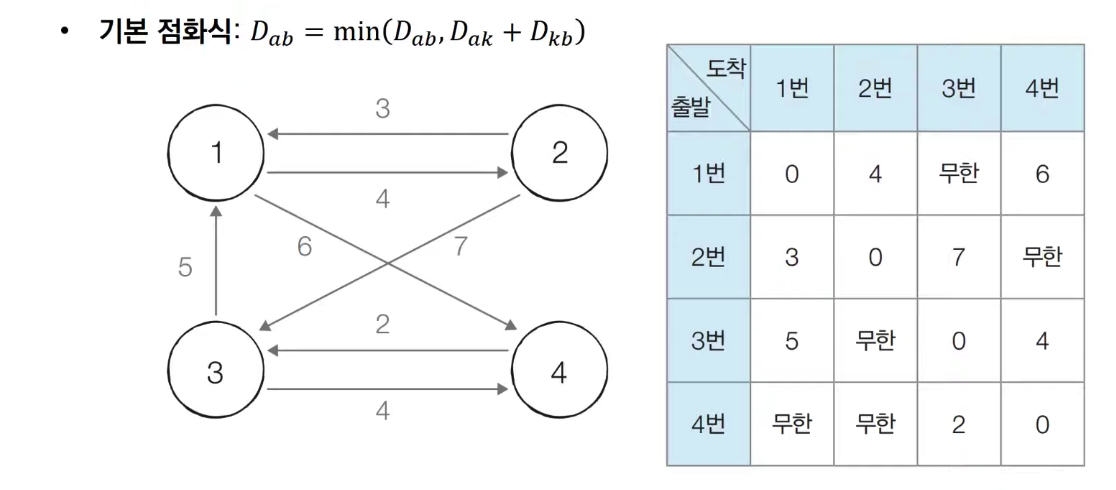
갱신하는 방법은 노드 a, k, b 가 있을 때,
a에서 b 이동 비용과 a, k, b 순서로 이동했을 때 비용 중 낮은 값으로 갱신합니다.

\[D_{ab} = min(D_{ab}, D_{ak} + D_{kb})\]

플로이드 워셜 진행 순서

• [준비] 2차원 배열에 간선 값을 초기화하고 출발과 도착이 같은 칸은 무한대로 초기화 합니다.

• [Step 1] 1번 노드를 거쳐가는 모든 경로를 갱신합니다.

• [Step 2] 2번 노드를 거쳐가는 모든 경로를 갱신합니다.

• [Step 3] 3번 노드를 거쳐가는 모든 경로를 갱신합니다.

• [Step 4] 4번 노드를 거쳐가는 모든 경로를 갱신합니다.

소스 코드

int distance[5][5] {
		{0, INF, 1, INF, 5},
		{3, 0, 9, 2, INF},
		{4, 4, 0, INF, INF},
		{INF, 8, 6, 0, INF},
		{INF, INF, INF, 2, 0}
	};

void FloydWarshall() {
	int node_count = 5;
	for (int node = 0; node < node_count; node++) {
		for (int i = 0; i < node_count; i++) {
			for (int j = 0; j < node_count; j++) {
                            distance[i][j] = min(
                                distance[i][j], 
                                distance[i][node] + distance[node][j]
                            );
			}
		}
	}
}