[Algorithm] 분할 정복 알고리즘 정리
분할 정복
분할 정복은 분할한 값들을 정복해 나가면서 해결하는 알고리즘입니다.
이를 활용한 대표적인 정렬 알고리즘은
이진 탐색, 합병 정렬, 퀵 정렬 등이 있습니다.
정렬 알고리즘 비교
|정렬 알고리즘|최대 실행 시간|최소 실행 시간|평균 실행 시간| |——|—|—|—| |선택 정렬| O(n^2)| O(n^2)| O(n^2)| |삽입 정렬| O(n^2)| O(n)| O(n^2)| |합병 정렬| O(nlg(n))| O(nlg(n))| O(nlg(n))| |퀵 정렬| O(n^2)| O(nlg(n))| O(nlg(n))|
분할 정복의 순서
- 분할하기 (Divide)
현재 문제를 작은 문제로 나누어(분할하여) 최대한 작은 문제까지 분할을 반복합니다. - 정복하기 (Conquer)
작은 문제가 된 것들을 모두 각자 해결합니다. (정렬, 탐색 등) - 통합하기 (Combine)
정복한 최소 문제들을 모아서 원하는 답을 구합니다.
분할 정복의 특징
- 분할된 작은 문제를 분할 전 문제와 성격이 동일합니다.
- 분할된 작은 문제는 서로 영향을 주지 않는 독립적 문제입니다.
- 재귀 호출에서 사용하는 Top-Down 방식과 유사합니다.
이진 탐색
이진 탐색 혹은 이분 탐색 이라고 불리는 이 탐색 방법은
정렬된 데이터가 배열에 저장되어 있을 때, 가장 높은 성능을 보여줍니다.
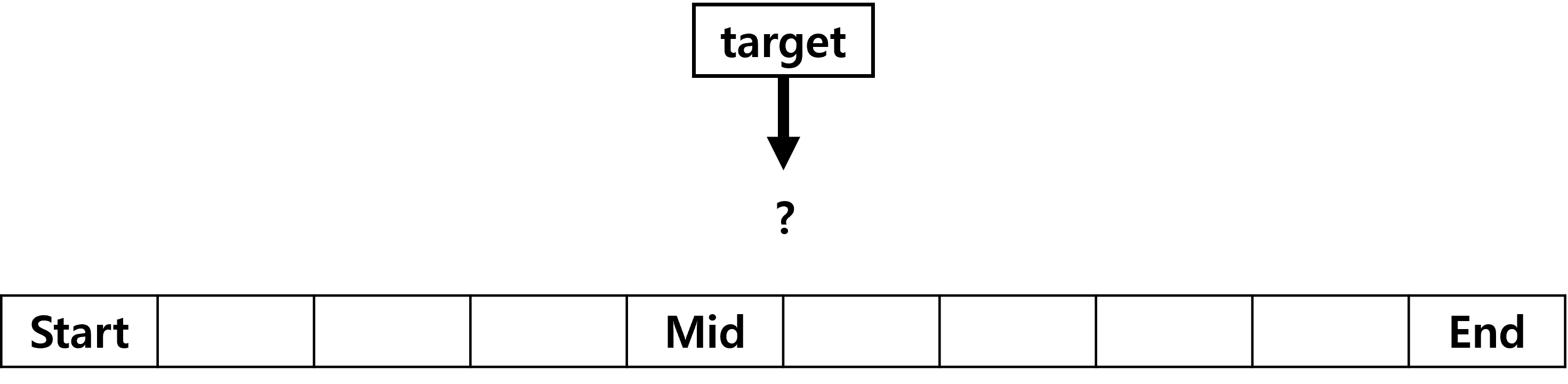
먼저 탐색의 시작, 중간, 종료 인덱스를 각각 저장하는 변수를 생성합니다.
그리고 탐색 값까지를 start, mid, end, target 이라는 변수에 저장한다고 하면
배열은 다음 그림과 같이 그려집니다.
위의 그림처럼 정렬된 배열과 변수가 준비되었으면 탐색을 시작할 준비는 끝났습니다.
탐색은 다음과 같은 순서로 진행됩니다. (단, 아래 설명은 배열이 오름차순 정렬이 되어있는 상태라는 전제입니다.)
1
2
3
4
5
1. mid 에 (start + end) / 2 값을 대입합니다.
2. mid 값과 target 값을 비교합니다.
a. target이 같으면 즉시 탐색을 종료합니다.
b. target이 작으면 start 부터 mid - 1 까지 탐색
c. target이 크면 mid + 1 부터 end 까지 탐색
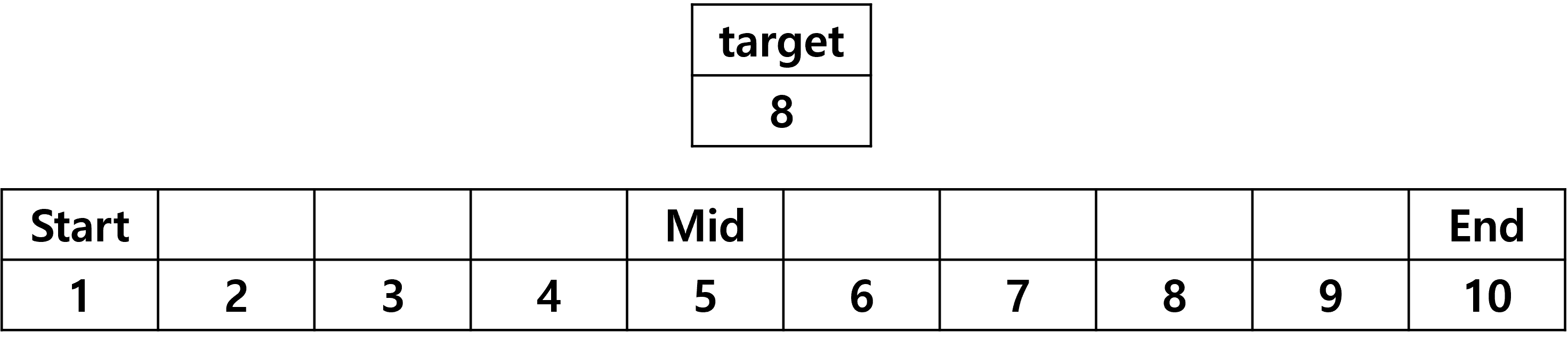
위의 그림에 맞춰 배열에 1부터 10까지 원소가 저장되어 있고
이 배열에 8 이 존재하는지 확인해보겠습니다.
먼저 start와 end의 중간값인 5 ((10 + 1) / 2) 위치에 mid 를 표시합니다.
그리고 mid와 target을 비교해 target이 크므로 start 위치값을 mid + 1 위치로 조정해줍니다.
그리고 다시 새로운 mid 값을 구해서 target과 비교합니다.
새롭게 구한 mid 가 target 과 동일하므로 탐색을 종료합니다.
이제 위의 순서도를 의사 코드로 표현하면 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
binary_search(start, end, target)
{
if(start > end)
return 0;
mid = (start + end) / 2
if(mid == target)
{
return mid;
}
else if(target < mid)
{
return binary_search(start, mid - 1, target);
}
else if(target > mid)
{
return binary_search(mid + 1, end, target);
}
}
위의 코드에서 범위 값이 mid - 1, mid + 1 로 전달하는 이유는
mid 를 비교하였을 때, 초과되거나 미만인 값이 target이므로 줄여서 보내는 것 입니다.
또한 탐색 범위가 역전되는 현상을 방지하고자 함수의 실행과 동시에 start와 end를 비교해야 합니다.
이제 C++코드로 직접 구현해 보겠습니다.
이분 탐색은 재귀문 혹은 반복문 모두 구현이 가능합니다.
그러나 재귀문의 경우 공간 복잡도가 높아질 수 있다는 단점 이 있기 때문에
가능하면 반복문으로 해결하는 것이 좋습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
int target;
int binary_search_recursive(int start, int end)
{
if(start > end)
return 0;
int mid = (start + end) / 2;
if(mid == target)
{
return mid;
}
else if(target < mid)
{
return binary_search(start, mid - 1);
}
else if(mid < target)
{
return binary_search(mid + 1, end);
}
}
int binary_search_loop(int start, int end)
{
int mid;
while(start < end)
{
mid = (start + end) / 2;
if(mid == target)
{
return mid;
}
else if(target < mid)
{
end = mid - 1;
}
else if(mid < target)
{
start = mid + 1;
}
}
return -1; // 범위 내 값이 없는 경우
}