[수학] 거리 측정법

백준 문제 에이티식스에서 제가 선택한 알고리즘은 BFS(너비 우선 탐색) 였습니다.

저거노트를 탄 신에이 노우젠(이하 신)이 전장에서 가능한 모든 레기온을 처치했을 때, 최소 소요시간을 구해야 하기 때문입니다.

그래서 최초의 코드는 다음과 같이 작성했습니다.

int BFS()
{
    bool** visited = new bool*[N];
    for(int y = 0; y < N; ++y) visited[y] = new bool[N]{ false };

    visited[start_y][start_x] = true;
    std::queue<std::pair<std::pair<int, int>, std::pair<int, int>>> q;

    // start_x, start_y : 현재 위치 
    // 0 : 경과 시간
    // target_cnt : 전체 레기온 수
    q.push(std::make_pair(std::make_pair(start_y, start_x), std::make_pair(0, target_cnt)));

    int total_time = 2e9;

    while(q.empty() == false)
    {
        auto curr = q.front();
        q.pop();

        for(int dir = 0; dir < 4; ++dir)
        {
            int new_y = curr.first.first + dy[dir];
            int new_x = curr.first.second + dx[dir];

            // 전장 밖 확인
            if(new_y < 0 || new_y >= N || new_x < 0 || new_x >= N)
                continue;
            
            // 이미 방문한 전장
            if(visited[new_y][new_x])
                continue;
            
            // 레기온 발견
            if(1 == board[new_y][new_x])
            {
                board[new_y][new_x] = 0;
                q.push(std::make_pair(std::make_pair(new_y, new_x), std::make_pair(curr.second.first + 1, curr.second.second - 1)));
            }

            // 레기온 없는 전장
            else
            {
                q.push(std::make_pair(std::make_pair(new_y, new_x), std::make_pair(curr.second.first + 1, curr.second.second)));
            }

            // 현재 위치 방문 기록
            visited[new_y][new_x] = true;
        }

        // 모든 레기온을 제거한 경우, 기록된 최소 시간과 비교
        if(curr.second.second == 0)
        {
            total_time = std::min(total_time, curr.second.first);
        }
    }

    return total_time;
}

그러나 이 코드의 문제점은 visited 배열을 사용하고 있기 떄문에 방문했던 위치를

다시 방문할 수 없다는 문제점이 있습니다.

재방문이 불가능하기 때문에 다음과 같은 전장에서는 정상적인 토벌이 불가능합니다.

// 1: 레기온, 2: 신
1 0 1
0 2 0
1 0 1

따라서 이 문제점을 해결하기 위해서 신의 위치에서

토벌 가능한 레기온 위치를 저장한 뒤 조합(Combination)을 통해 순서를 결정하고

이 순서로 토벌했을 때, 레기온 토벌 최소 시간을 구하고자 하였습니다.

이 과정에서 중요한 것은 신의 위치에서 토벌 가능한 레기온 위치 판별법 입니다.

위치 판별을 위해 대표적인 거리 측정법인 유클리드 측정법과 맨해튼 측정법, 체스판 거리 측정법을 알아보겠습니다.

유클리드 측정법

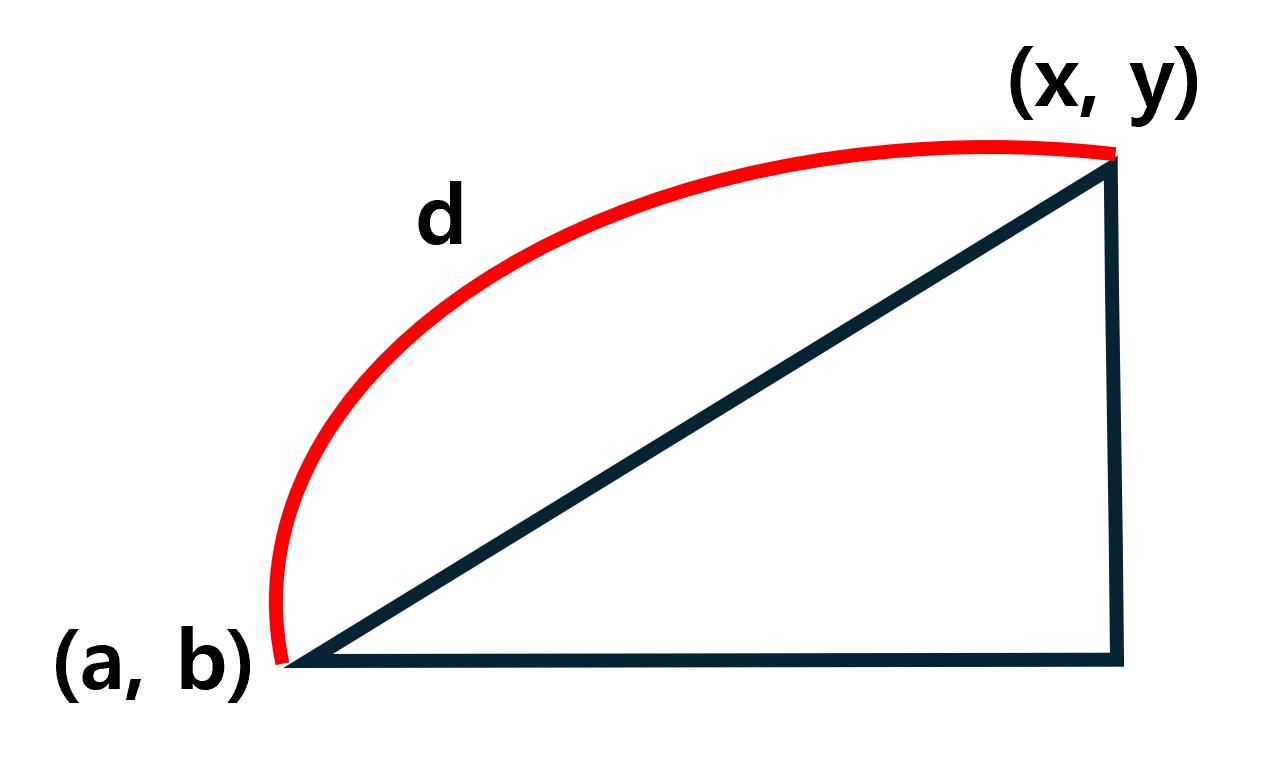
피타고라스 정리만 알고 있다면, 유클리드 측정법도 이미 알고 있다고 할 수 있습니다.

위의 그림에서 d 가 바로 유클리드 거리 입니다.

맨해튼 거리

맨해튼 거리는 체스판 혹은 바둑판과 같은 일정한 칸이 있는 맵에서 사용되는 방법입니다.

점(x, y)과 점(a, b) 사이 맨해튼 거리 측정법은 매우 간단합니다.

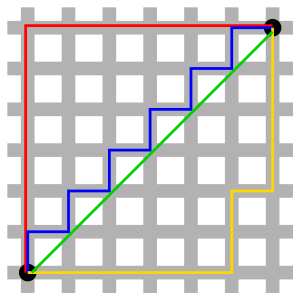
위의 그림에서 최단거리는 초록색 처럼 보이지만

회색 경로를 반드시 이용해서 목적지까지 가고자 한다면 파랑색이 최단거리가 될 수 있습니다.

뿐만 아니라 노랑색, 빨강색 경로도 최단거리가 될 수 있습니다.

실제 이동 거리는 파랑, 빨강, 노랑 모두 같기 떄문입니다.

따라서 맨해튼 거리 측정법은 다음과 같습니다.

x - a

+

y - b

체스판 거리 측증법

체스판 거리는 두 벡터값의 차이가 가장 큰 것으로 정의됩니다.

max(

x1 - y1

,

x2 - y2

, …,

xn - yn

)

최종 코드

위의 3가지 거리 측정법을 이용해 다음과 같은 코드로 수정하였습니다.

#include <iostream>
#include <vector>
#include <algorithm>

int main()
{
    int N, start_x, start_y;
    std::cin.tie(0)->sync_with_stdio(false);
    std::cin >> N;

    std::vector<std::pair<int, int>> enemy;
    for(int y = 0; y < N; ++y)
    {
        for(int x = 0, temp; x < N; ++x)
        {
            std::cin >> temp;
            if(2 == temp)
            {
                start_x = x;
                start_y = y;
            } else if(1 == temp)
            {
                enemy.push_back(std::make_pair(y, x));
            }
        }
    }

    if(true == enemy.empty())
    {
        printf("Undertaker\n0");
        return 0;
    }

    std::vector<std::pair<int, int>> target;
    for(auto t : enemy)
    {
        if((0 == (std::abs(start_x - t.second) + std::abs(start_y - t.first)) % 2)
        || 
        (((start_x + start_y) % 2) == ((t.first + t.second) % 2)))
        {
            target.push_back(t);
        }
    }

    if(target.size() == enemy.size()) 
    {
        int MIN_TIME = 2e9;

        do{
            int wid = std::abs(start_x - target[0].second);
            int hei = std::abs(start_y - target[0].first);
            int curr_time = std::max(wid, hei);
            
            for(int i = 1; i < target.size(); ++i)
            {
                curr_time += std::max(std::abs(target[i].second - target[i - 1].second),
                        std::abs(target[i].first - target[i - 1].first));
            }

            MIN_TIME = std::min(MIN_TIME, curr_time);
        }
        while(std::next_permutation(target.begin(), target.end()));  
        
        printf("Undertaker\n%d", MIN_TIME);
    }
    else
    {
        printf("Shorei");
    }

    return 0;
}

참고

거리 척도 방법 소개
맨해탄 거리 측정법