[자료구조] Heap(힙)의 개념

힙(Heap) 자료구조란

완전 이진 트리를 사용한 자료구조로 주로 우선순위를 표현하기 위해 사용됩니다.
힙의 구현 방법에 따라 최댓값 혹은 최솟값을 빠르게 찾을 수 있습니다.

최댓값을 빠르게 구하기 위한 힙을 최대 힙이라고 하며,
최솟값을 빠르게 구하기 위한 힙을 최소 힙이라고 합니다.

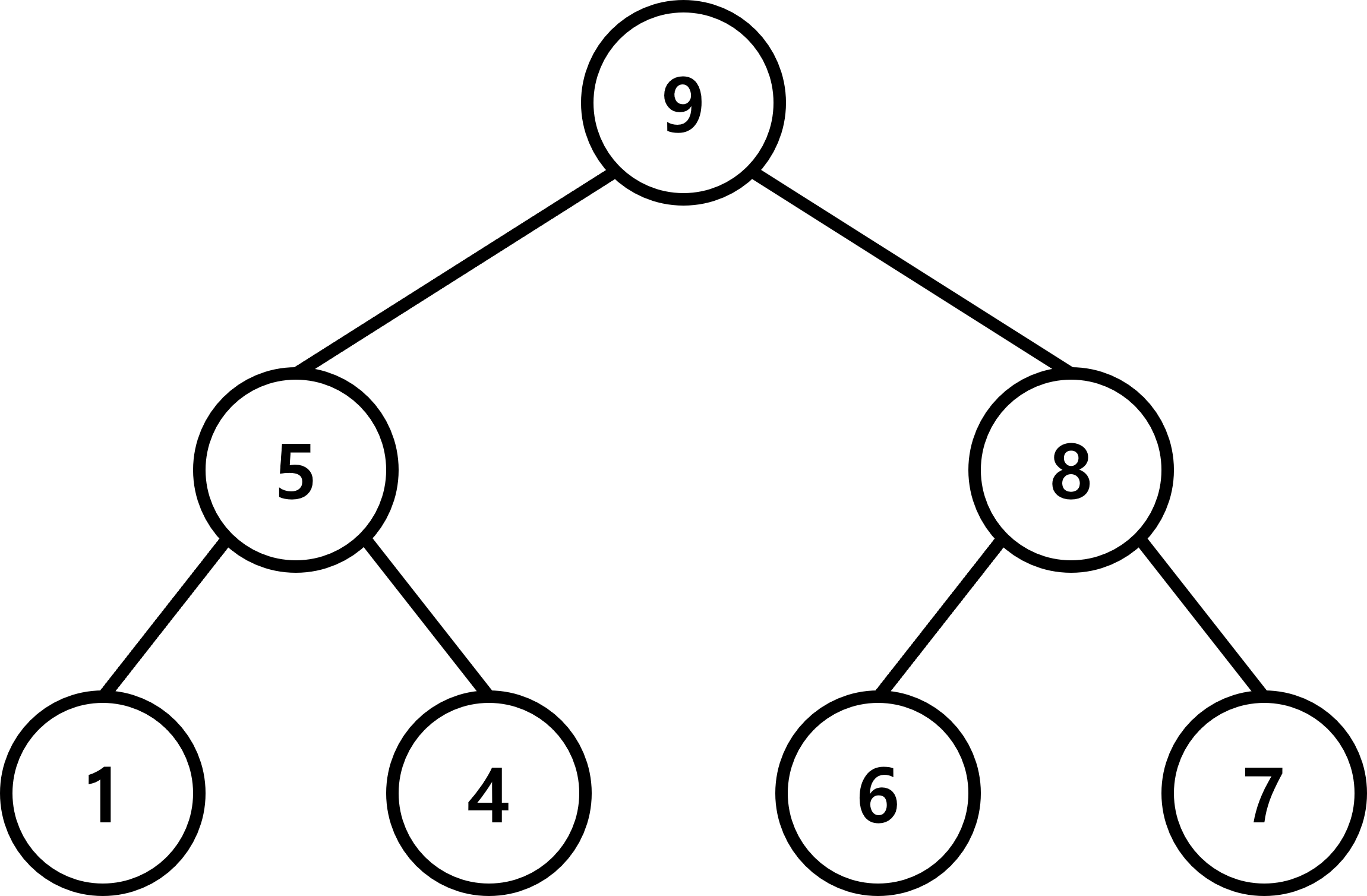
최대 힙

최댓값을 빠르게 구할 수 있는 최대 힙은 루트 노드에 최댓값을 저장합니다.
그리고 노드의 깊이가 깊어질수록(높이가 낮아질수록) 숫자가 작아지는
내림차순 순서로 표현됩니다.

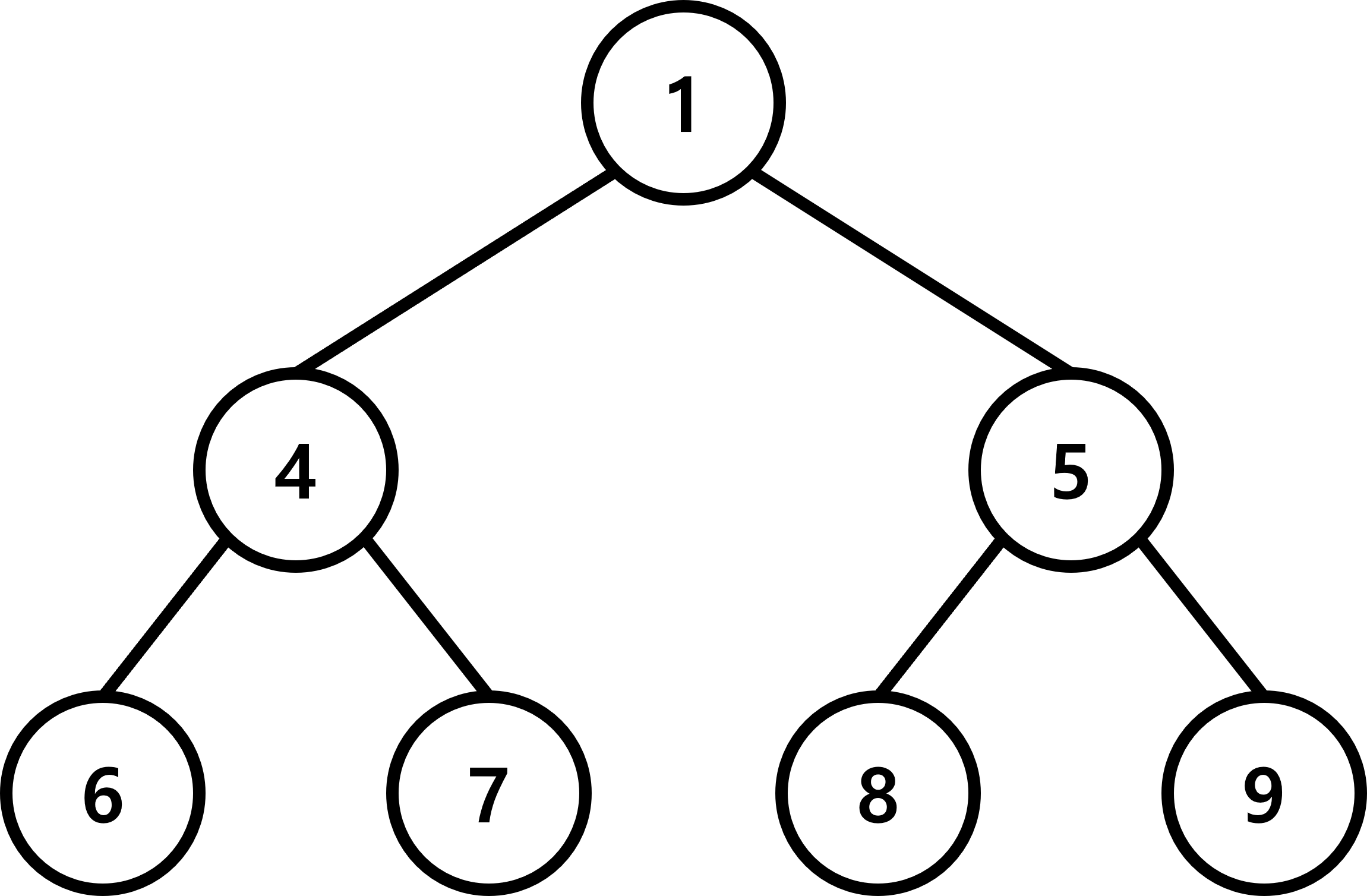
최소 힙

최대 힙과 반대로 최솟값을 빠르게 확인할 수 있는 자료구조가 최소 힙 입니다.
최소 힙은 루트 노드에 최솟값을 저장합니다.
그리고 노드의 깊이가 깊어질수록(높이가 낮아질수록) 숫자가 커지는 오름차순으로 표현됩니다.

힙 표현하기

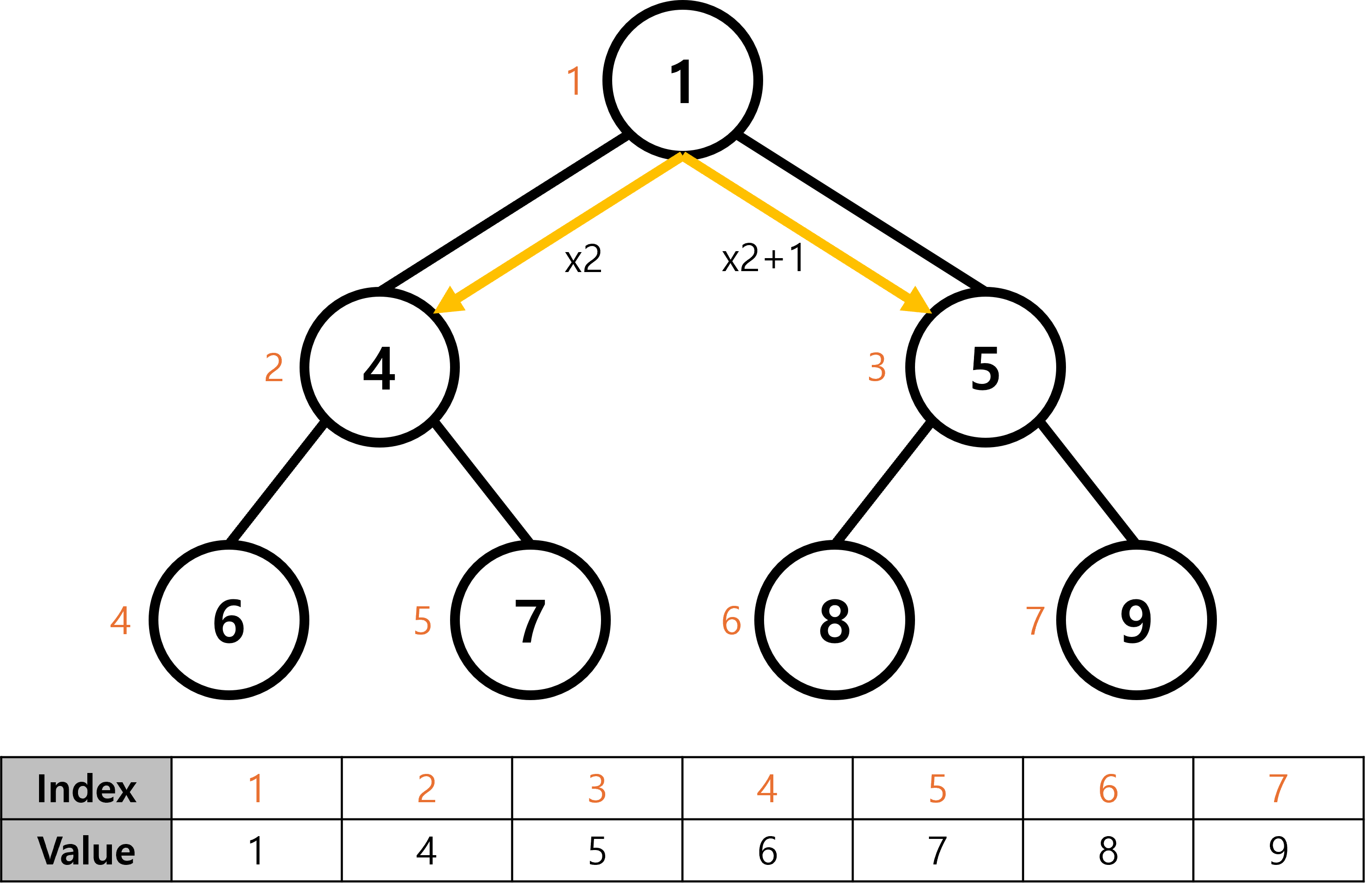
힙은 완전 이진 트리라는 특징을 활용해서 배열로 구현할 수 있습니다.

• \[(왼쪽 자식 인덱스) = (부모 인덱스) \times 2\]
• \[(오른쪽 자식 인덱스) = (부모 인덱스) \times 2 + 1\]
• \[(부모 인덱스) = (자식 인덱스) / 2\]

힙 구현하기 (C++ STL)

C++로 구현하기 가장 쉬운 힙은 queue에 있는 priority_queue(우선순위 큐)가 있습니다.
이 자료구조는 큐 라는 이름을 갖고 있지만 내부의 구현은 최대 힙을 사용하고 있습니다.

우선순위 큐를 사용하면서 주의할 점은 최대 힙을 사용한다는 것입니다.
만약, 최소 힙을 사용하는 다익스트라 최단거리 알고리즘에서 우선순위 큐를 사용하려면
값을 입력할 때, 음수 부호를 붙여 push하면 최대 힙을 최소 힙처럼 사용할 수 있습니다.

#include <iostream>
#include <queue>

using namespace std;

int main() {
    priority_queue<int> pq;
    pq.push(10);
    pq.push(20);
    pq.push(15);
    pq.push(30);
    pq.push(25);

    // 최대 힙에서 최댓값: 30
    cout << "최대 힙에서 최댓값: " << pq.top() << endl;
    pq.pop();

    // 새로운 최댓값: 25
    cout << "새로운 최댓값: " << pq.top() << endl;

    pq.push(99);

    // 새로운 최댓값: 99
    cout << "새로운 최댓값: " << pq.top() << endl;

    return 0;
}

우선순위 큐가 아닌 최대 힙 구현으로는 C++ STL의 make_heap() 함수가 있습니다.
이 함수는 전달받은 컨테이너를 최대 힙으로 정렬하는 역할을 합니다.

그러나 내부 메서드로 최댓값을 제거하는 우선순위 큐와 다르게
make_heap으로 만든 힙은 최댓값을 제거하기 위해서 pop_heap이라는 함수를 사용해야 합니다.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main() {
    vector<int> vec{10, 20, 15, 30, 25};

    make_heap(vec.begin(), vec.end());
    cout << "최대 힙에서 최댓값: " << vec.front() << endl;

    // 벡터는 원소의 삭제가 뒤에서만 발생하므로(.pop_back())
    // 최댓값을 맨 뒤로 이동
    pop_heap(vec.begin(), vec.end());
    vec.pop_back();

    cout << "새로운 최댓값: " << vec.front() << endl;

    vec.push_back(99);
    push_heap(vec.begin(), vec.end());

    cout << "새로운 최댓값: " << vec.front() << endl;

    return 0;
}

힙 단점

최대 힙, 최소 힙은 각자 최댓값과 최솟값을 빠르게 구할 수 있는 이유는
새로운 원소가 힙에 삽입되었을 때, 매번 새롭게 정렬되기 때문입니다.

힙 자료구조는 새로운 원소가 삽입될 때 마다 새롭게 정렬됩니다.
정렬은 삽입 뿐만 아니라 원소 제거에서도 발생할 수 있습니다.

따라서 힙 자료구조는 조회에서는 우수한 성능을 보여주지만
삽입, 삭제가 자주 발생한다면 사용이 적합하지 않을 수 있습니다.