[자료구조] 이진 탐색 트리

이진 트리를 이용한 탐색

이전 포스트에서 이진 트리에 대해 알아보았습니다.
이번 포스트에서는 이진 트리를 활용한 이진 탐색 트리에 대해 알아보겠습니다.

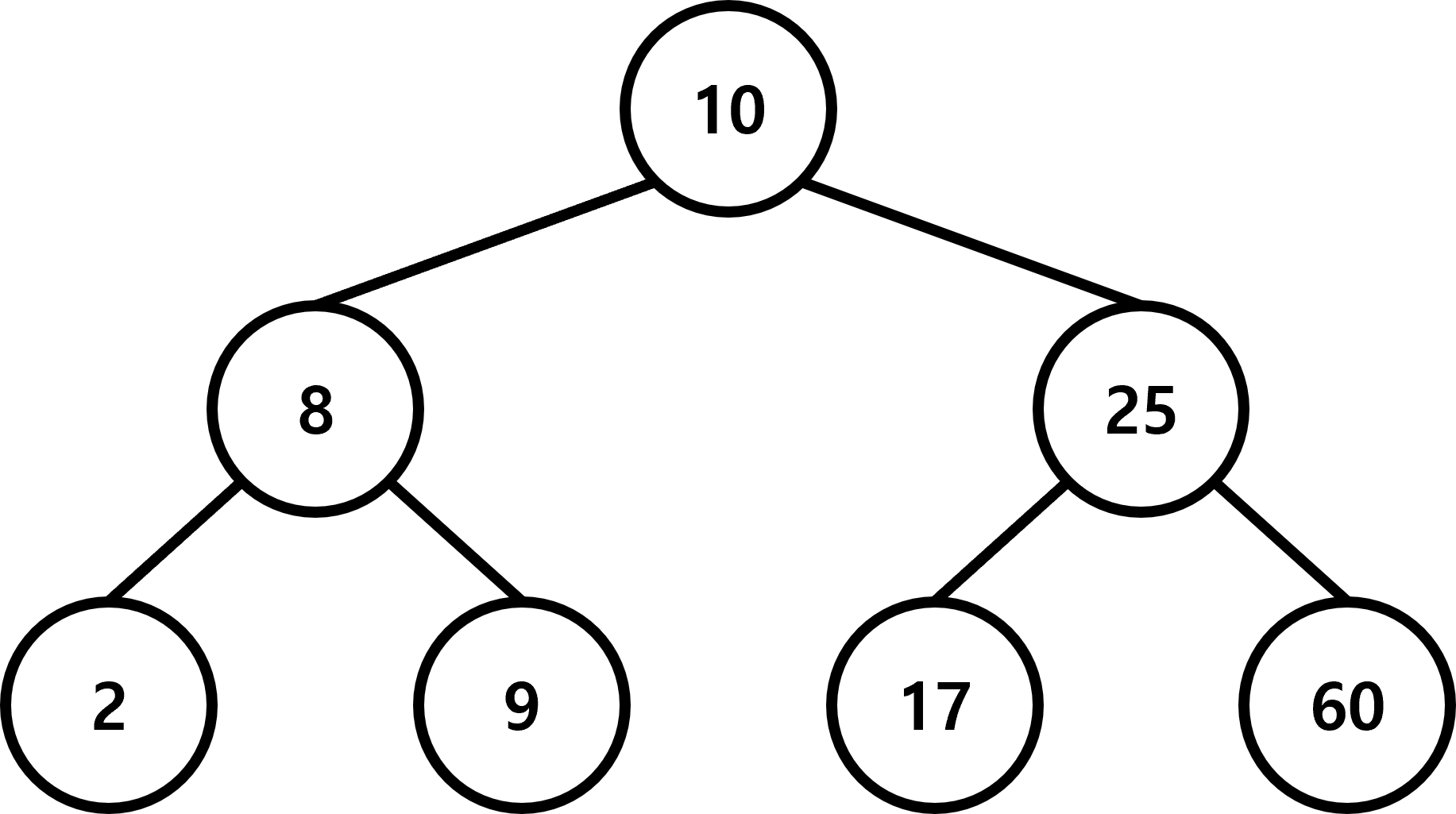
이진 탐색 트리는 다음과 같은 특징이 있습니다.

• 키 중복 없음
• 특정 노드의 왼쪽 서브 트리는 특정 노드 보다 작은 키 값만 존재
• 특정 노드의 오른쪽 서브 트리는 특정 노드 보다 큰 키 값만 존재
• 모든 서브 트리는 이진 탐색 트리

탐색 시간

위와 같은 특징들 덕분에 이진 탐색 트리는 탐색 에서 빠른 속도를 보여줍니다.
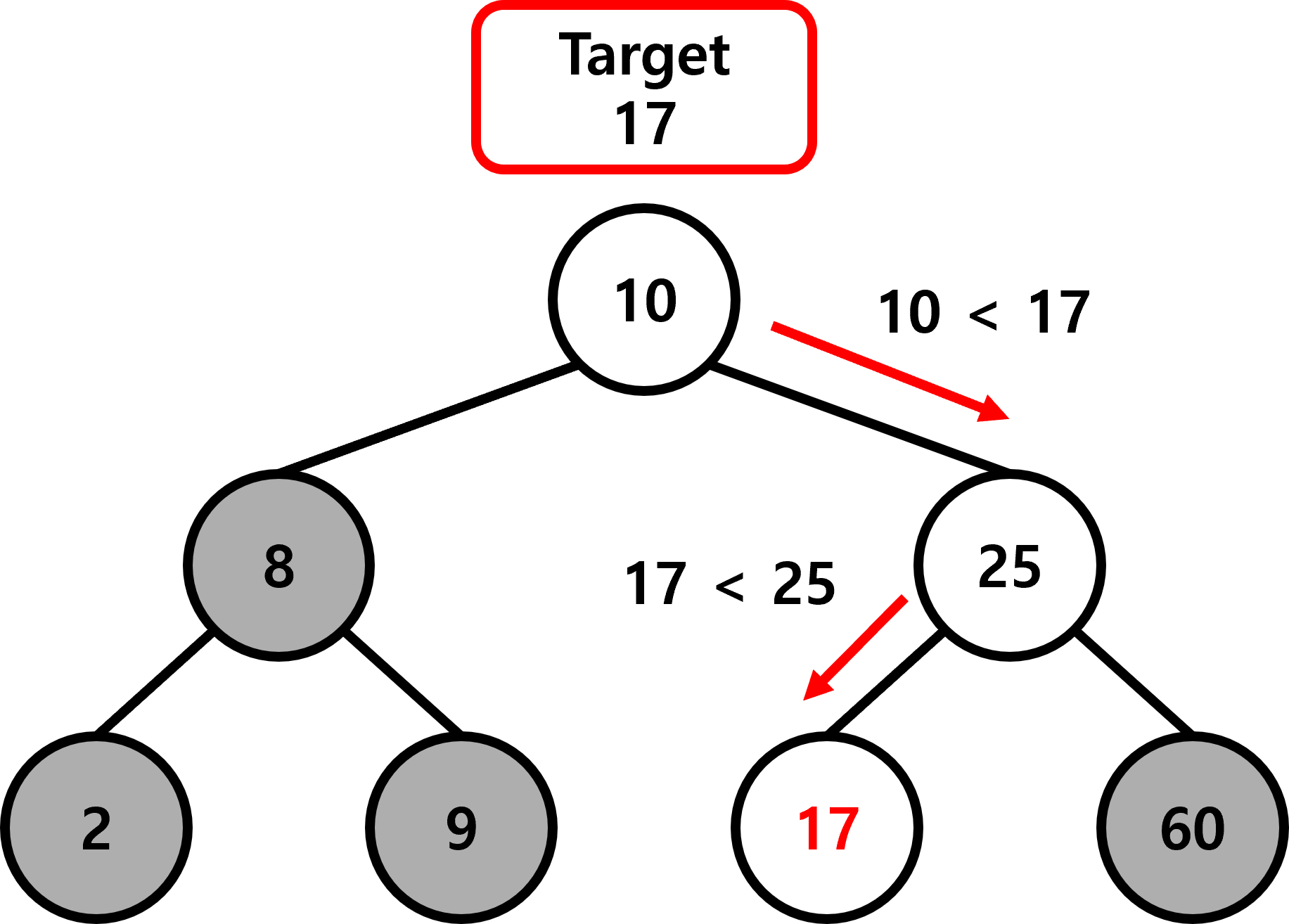
이진 탐색 트리가 탐색하는 방법은 아래와 같습니다.

시간 복잡도 계산을 위해 포화 이진 트리에서
찾고자 하는 키 값을 target, 각 노드에 저장된 키 값을 value 라고 하겠습니다.

1. 현재 방문한 노드의 value 와 target을 비교
2. target이 value 보다 작으면 현재 노드의 왼쪽 서브 트리를 탐색,
   target이 value 보다 크면 현재 노드의 오른쪽 서브 트리를 탐색

위 방법을 반복적으로 수행하여 target이 존재하는지 탐색합니다.
2번에서 왼쪽 서브 트리, 오른쪽 서브 트리 중 하나를 선택하게 됩니다.
이 선택으로 비교해야 하는 노드의 개수가 절반씩 줄어듭니다.

탐색을 진행하면서 이전 노드로 돌아가거나 같은 높이에 있는 노드를 탐색하지 않으므로
탐색하는 노드의 개수는 트리의 높이와 같습니다.
포화 이진 트리의 높이는 노드의 개수가 N, 높이가 h 일때, 둘의 관계는 다음과 같습니다.

\[N = 2^{(h + 1)} - 1\]

이 식을 정리하여 h 에 대한 계산식으로 정리하면 다음과 같습니다.

\[N + 1 = 2^{(h + 1)}\] \[log(N + 1) = log(2^{(h + 1)})\] \[log(N + 1) = h + 1\] \[log(N + 1) - 1 = h\]

탐색하는 노드의 수가 트리의 높이와 같다고 하였으므로
이진 탐색 트리의 탐색 연산 시간 복잡도는 아래와 같습니다.

\[O(h) = O(log(N))\]

삽입 연산 방법

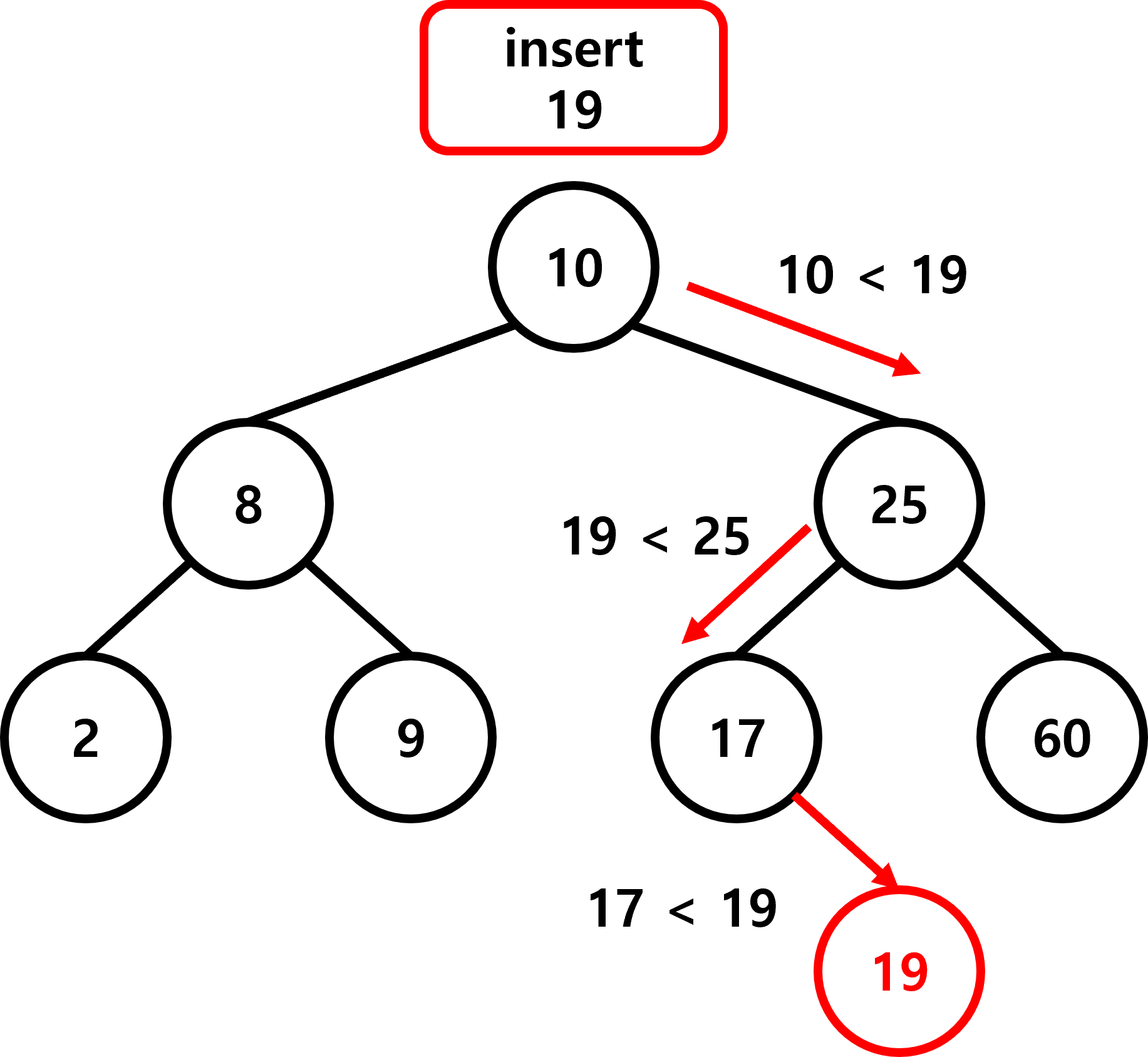
이진 탐색 트리는 중복을 허용하지 않으므로 모든 키 값은 서로 크거나 같습니다.
이진 탐색 트리에 새로운 값을 넣을 때는 키 값을 비교하면서 삽입할 위치를 찾으면 됩니다.

1. 현재 키 값과 비교해 삽입 키 가 작으면 왼쪽 서브 트리로, 크면 오른쪽 서브 트리로 이동
2. 더 이상 비교할 대상이 없으면 그 자리에 삽입하면 됩니다.

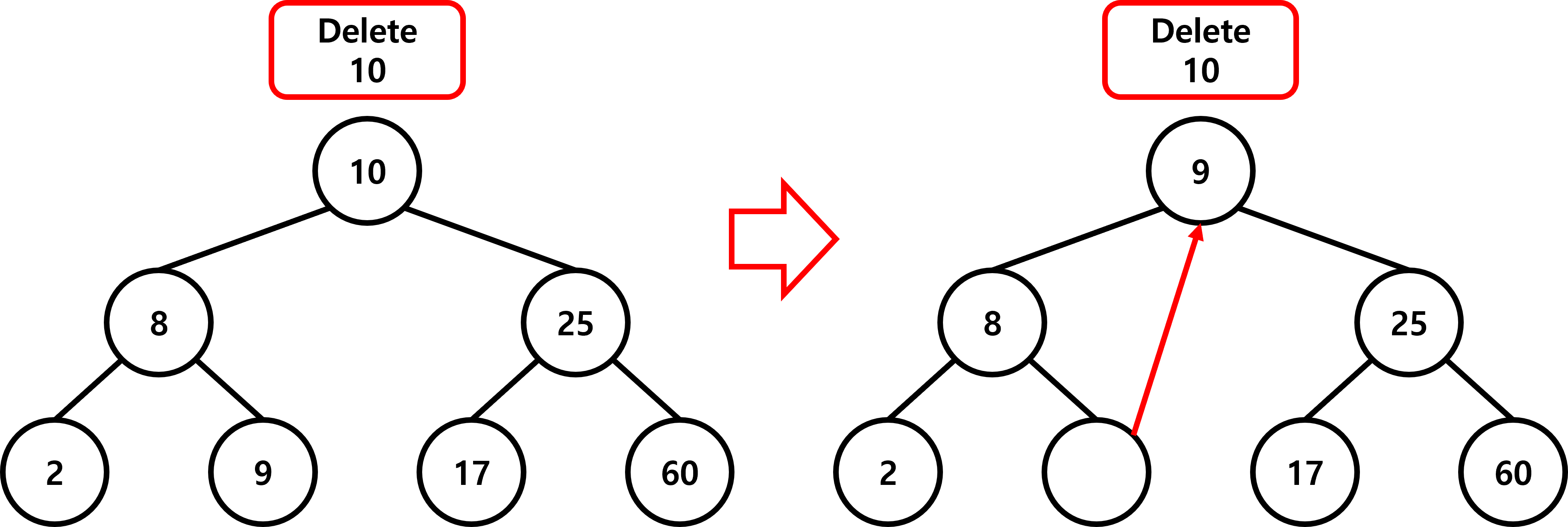
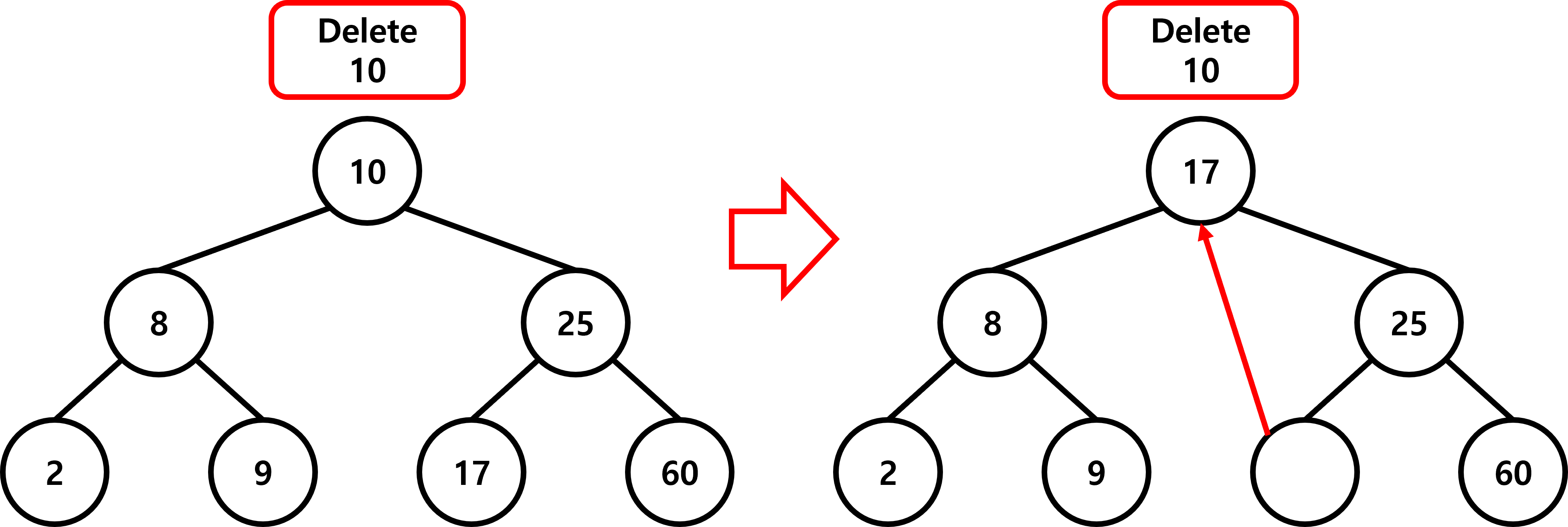
삭제 연산 방법

이진 탐색 트리에서 삭제되는 노드가 트리 내부에 존재하지만 전처리 없이 삭제할 경우
트리 자체가 망가질 수 있습니다.
따라서 삭제해야 하는 노드의 위치에 따라 삭제 방법이 다릅니다.

삭제 노드의 자식 수	노드 삭제 방법
2	왼쪽 서브 트리의 최대 키 값, 오른쪽 서브 트리의 최소 키 값 중 하나를 삽입
1	1개의 자식 노드를 삭제 노드 위치로 삽입
0	전처리 없이 바로 삭제

[왼쪽 서브 트리의 최대 키 값으로 교체]

[오른쪽 서브 트리의 최소 키 값으로 교체]