[자료구조] 이진 트리

이진 트리의 개념

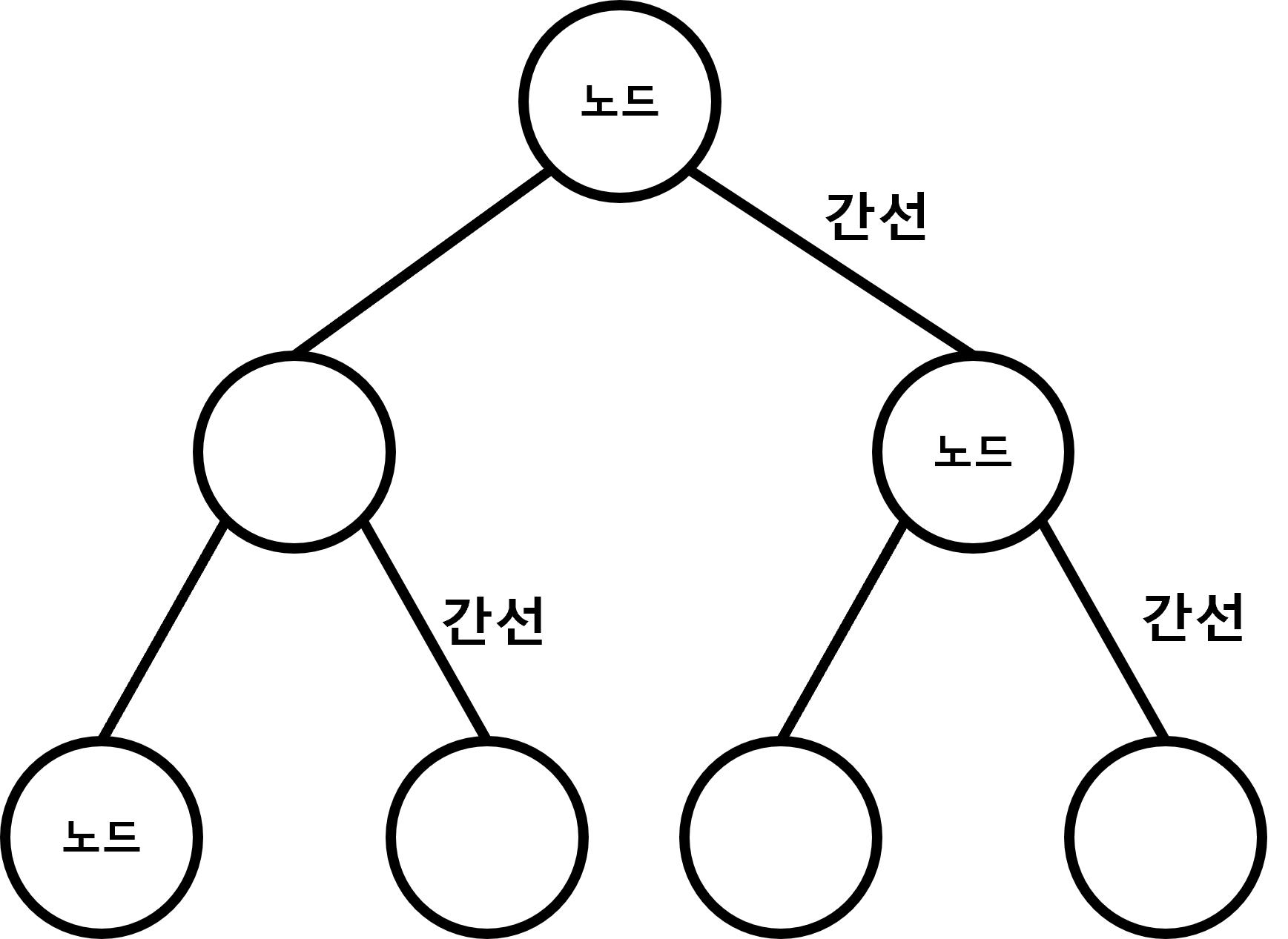
이진 트리는 최대 차수가 2 인 트리입니다.
즉, 트리에 있는 모든 노드는 자식 노드의 수가 2개 이하로 갖고 있는 경우입니다.
2개 이하라고 한 이유는 트리 모양에 따라 이름이 다르기 때문입니다.
대표적으로 정 이진 트리, 포화 이진 트리, 완전 이진 트리, 균형 이진 트리 등이 있습니다.

[모든 노드의 차수가 2인 이진 트리]

정 이진 트리

정 이진 트리(Full Binary Tree)는 트리의 모든 노드가 자식을 2개 갖거나 없는 트리를 일컫습니다.

[모든 노드의 차수가 2 혹은 0이므로 정 이진 트리]

포화 이진 트리

포화 이진 트리(Perfect Binary Tree)는 모든 레벨에서 노드들이 모두 채워져 있는 이진 트리를 일컫습니다.
트리의 높이가 k 라면 포화 이진 트리의 노드의 총 개수는 \(2^k - 1\) 개 입니다.

완전 이진 트리

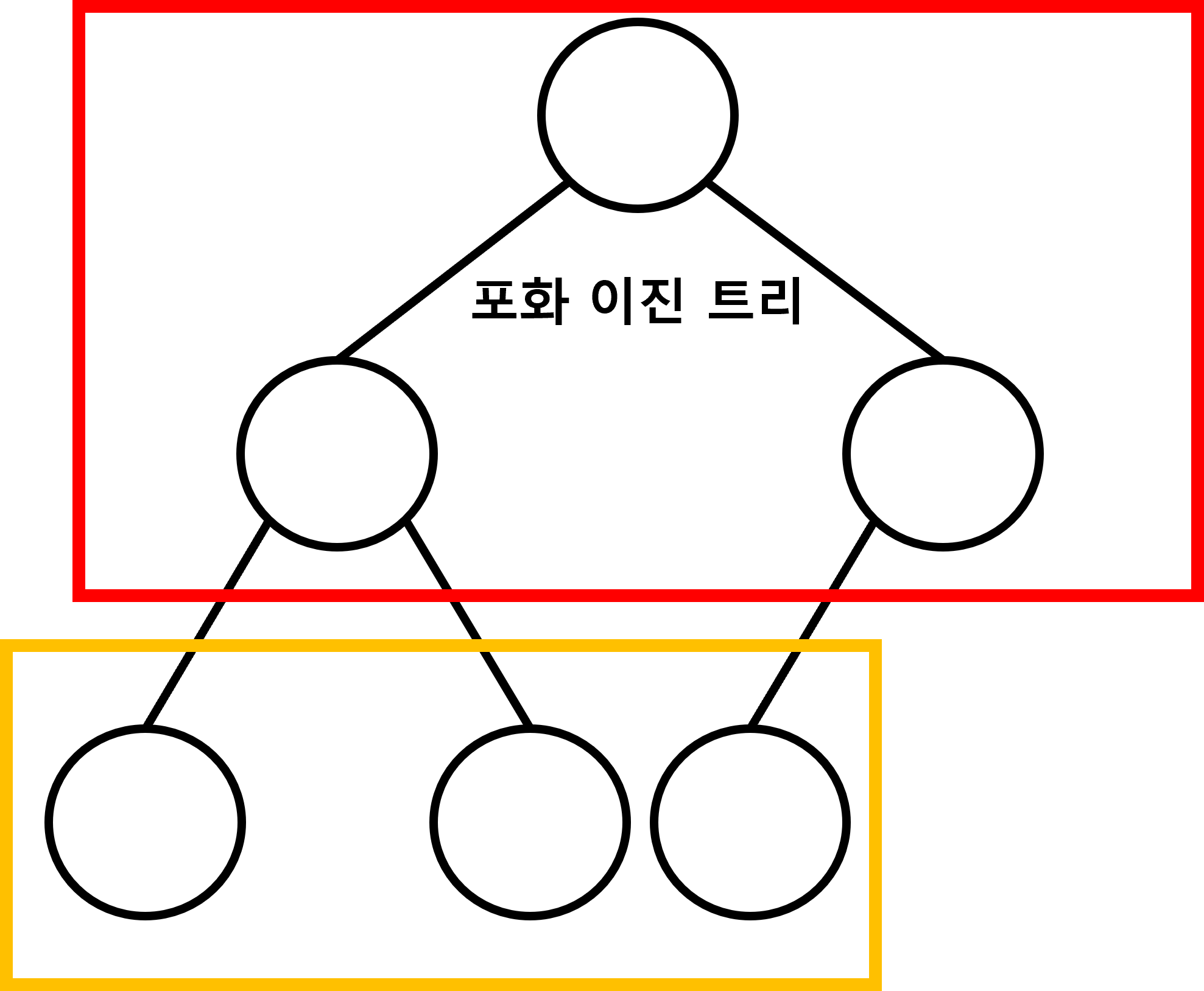
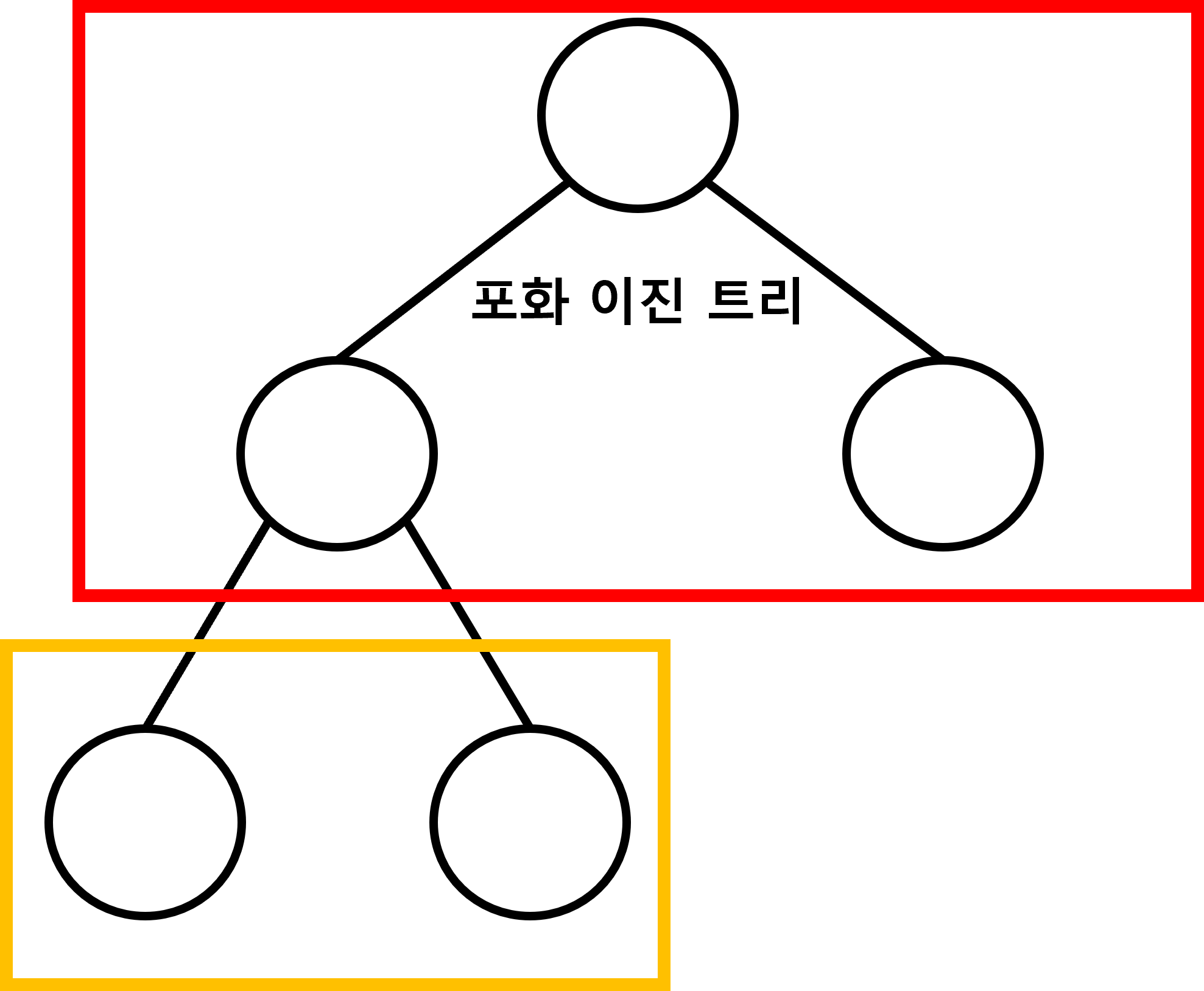
완전 이진 트리(Complete Binary Tree)는 포화 이진 트리에서 오른쪽 리프 노드를 제거해 나간 트리입니다.
트리의 높이가 k 일때, 깊이가 k - 1까지는 포화 이진 트리이고 깊이 k 에서는 가장 왼쪽 리프 노드부터
차례대로 채워져 있으면 모두 완전 이진 트리 입니다.
따라서 아래의 그림 모두 완전 이진 트리입니다.

[완전 이진 트리]

[완전 이진 트리]

[완전 이진 트리]

완전 이진 트리에서 노드의 개수는 트리의 높이가 h 일 때 \(2^h <= (노드 개수) < 2^(h + 1)\) 사이 값 하나 입니다.

이진 트리의 약점

[최악의 이진 트리]

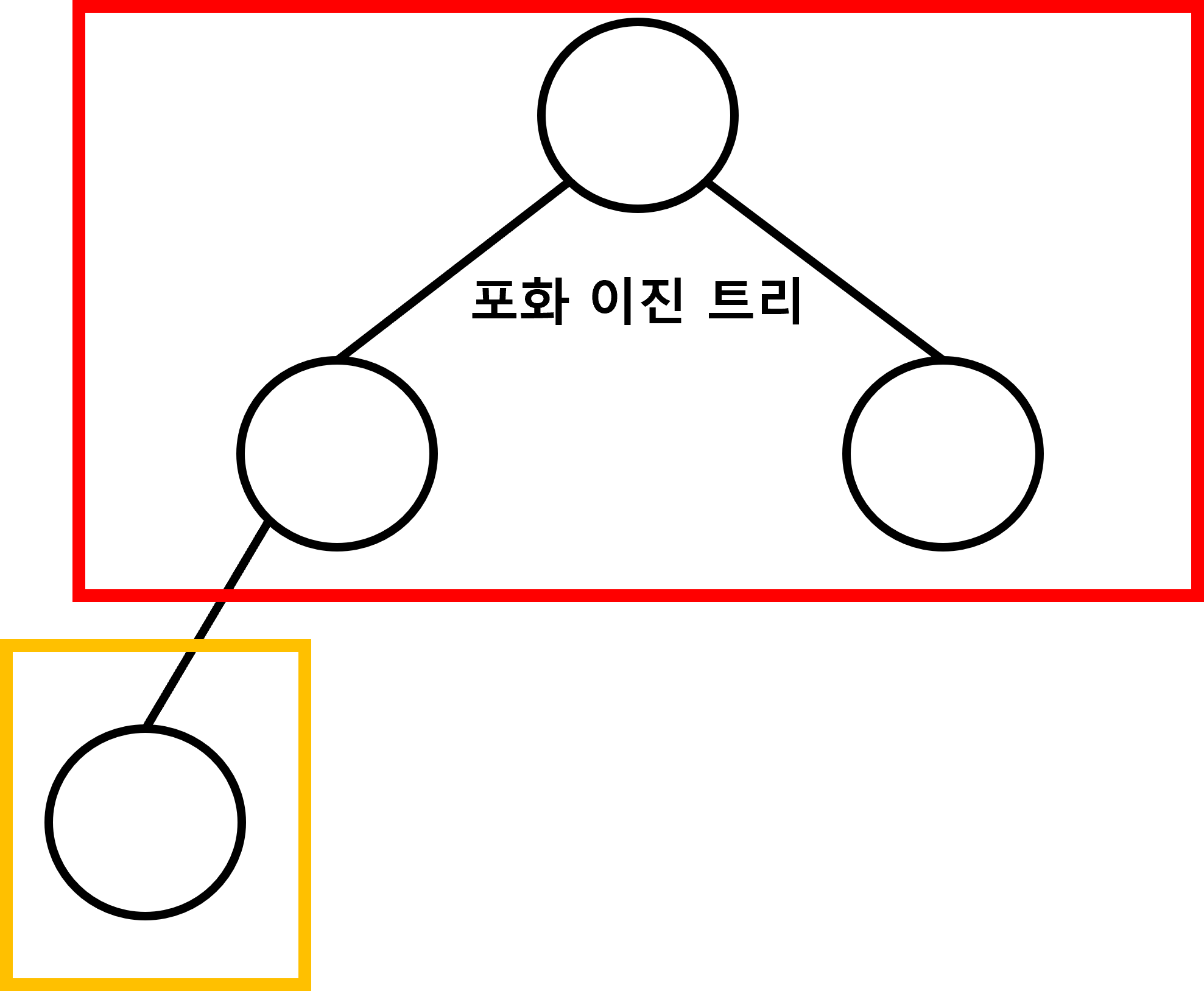
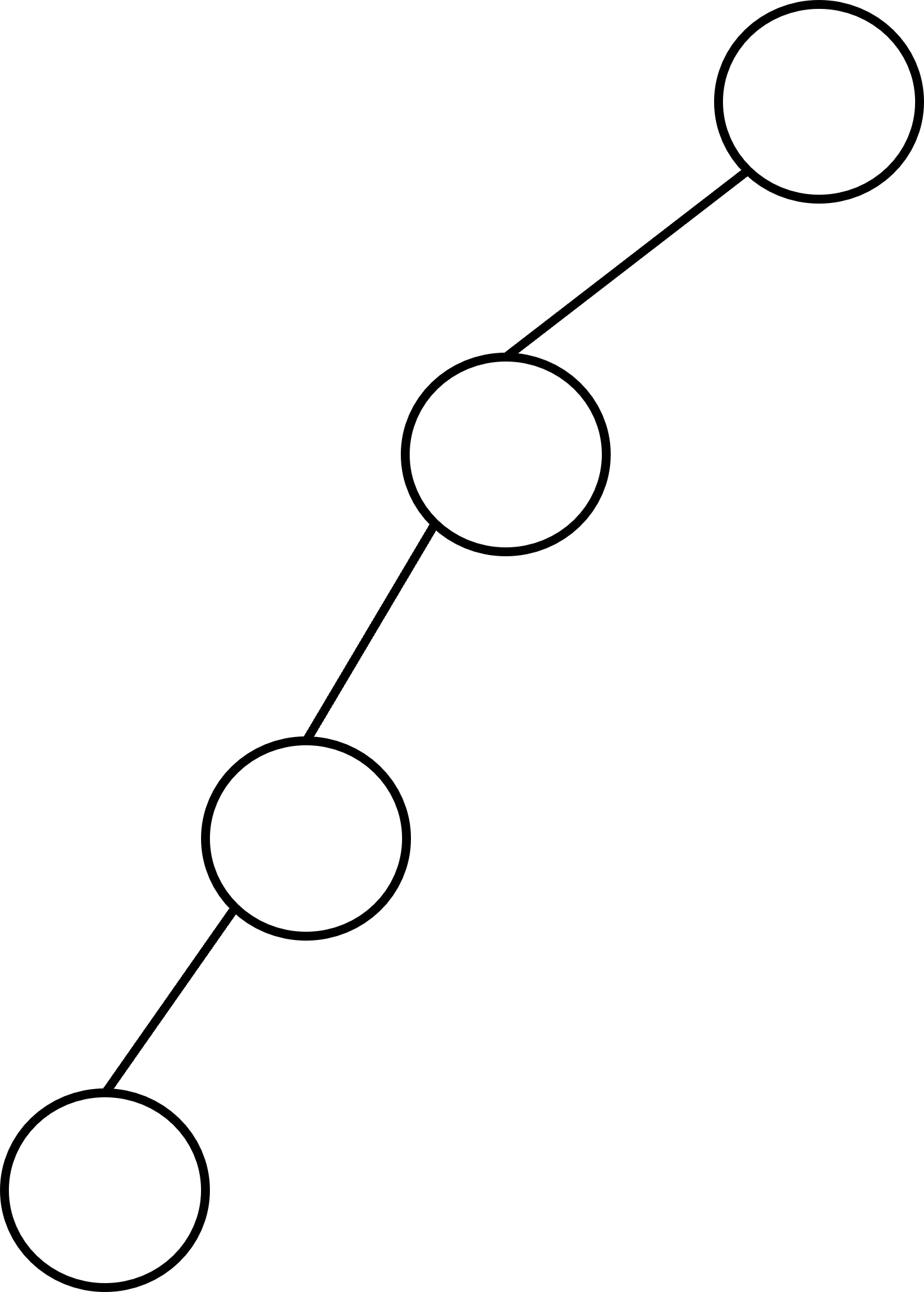
만약 그림처럼 이진 트리가 만들어질 경우, 모든 노드에는 사용하지 않는 오른쪽 자식 노드 포인터가 낭비되고
데이터를 탐색, 삭제, 삽입할 때 O(N) 이라는 속도가 될 것입니다.
따라서 이 문제점을 보완하고자 제시된 것이 스스로 균형을 맞추는 균형 이진 트리 입니다.

균형 이진 트리는 최대힙, 최소힙 등 여러 알고리즘 에서 사용되므로 다른 포스트에서 자세히 다루겠습니다.

이진 트리의 순회

이진 트리의 순회는 기본 트리 순회 방법과 동일합니다.

// 노드 구조체
struct NODE {
    char data;
    NODE* left;
    NODE* right;
};

// 전위 순회
void preorder(NODE* curr) {
    if(curr != nullptr) {
        cout << curr->data << endl;   // 데이터 출력
        preorder(curr->left);
        preorder(curr->right);
    }
}

// 중위 순회
void inorder(NODE* curr) {
    if(curr != nullptr) {
        inorder(curr->left);
        cout << curr->data << endl;   // 데이터 출력
        inorder(curr->right);
    }
}

// 후위 순회
void postorder(NODE* curr) {
    if(curr != nullptr) {
        postorder(curr->left);
        postorder(curr->right);
        cout << curr->data << endl;   // 데이터 출력
    }
}