[알고리즘] 이진 탐색

이것이 취업을 위한 코딩 테스트다 with 파이썬 (나동빈 저) 를 참고해 작성한 포스트입니다.

순차 탐색

여러 탐색 알고리즘 중 가장 가장 기본적인 탐색이 순차 탐색입니다.
순차 탐색은 이름처럼 특정한 데이터를 찾기 위해 앞에서부터 하나씩 차례대로 확인하는 알고리즘 입니다.
보통 정렬되지 않은 배열에서 탐색하기 위해 사용하며
데이터의 개수가 N개 일 때, \(O(N)\) 이라는 시간 복잡도를 갖고 있습니다.

int arr[5]{2, 5, 1, 4, 3};
int target = 4;

for(int i = 0; i < 5; ++i)
{
    // 데이터를 하나씩 확인
    if(target == arr[i])
    {
        cout << arr[i];
        break;
    }
}

이진 탐색

순차 탐색은 정렬에 상관하지 않고 \(O(N)\) 시간 복잡도에서 탐색하는 알고리즘 이였습니다.
이번에 설명하는 이진 탐색은 순차 탐색과 다르게 배열이 반드시 정렬되어 있어야 동작이 하지만
탐색 범위가 절반씩 감소 하는 특징 덕분에 \(O(log(N))\) 매우 빠른 시간 복잡도를 갖고 있습니다.

이진 탐색에서는 시작점, 중간점, 끝점 3개의 변수로 동작하며
찾으려는 데이터와 중간점을 반복 비교하여 원하는 데이터를 탐색합니다.

10개의 값이 채워진 배열에서 4 라는 값을 이진 탐색으로 찾으면 다음과 같이 진행됩니다.

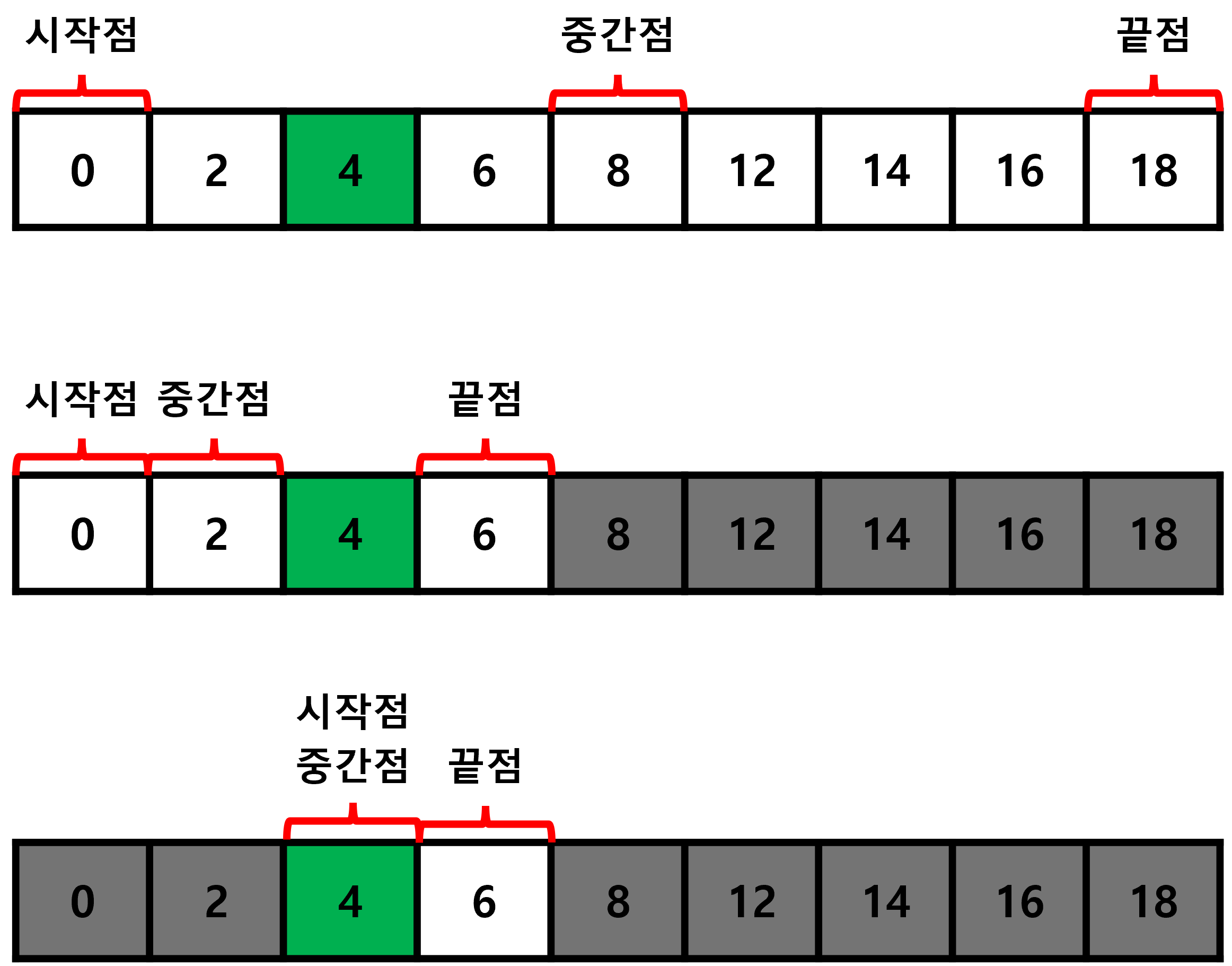
첫 번째 배열에서는 시작점과 중간점 그리고 끝점을 배치합니다.
시작점과 끝점은 각각 시작 인덱스와 마지막 인덱스를 갖고 있고
중간점은 시작 인덱스와 마지막 인덱스의 중간값을 갖습니다.

\[\frac{(0 + 9)}{2} = 4.5\]

이때, 인덱스의 값은 항상 자연수이므로 소수점 이하는 버림으로 계산합니다.
따라서 중간값은 4를 갖습니다.

중간값(인덱스 4)가 가르키는 값이 8이고 찾고자 하는 값이 4 이므로
중간값의 왼쪽 범위 에 4가 있음을 예상할 수 있습니다.

이번에는 끝점을 이동시키고 중간값을 새롭게 구해 다시 비교합니다.
이 과정을 반복 해 중간값이 가르키는 값이 4 가 되면 탐색을 종료합니다.

int arr[10]{0, 2, 4, 6, 8, 10, 12, 14, 16, 18};

bool recursive_binary_search(int target, int start, int end)
{
    if(start > end)
    {
        return false;
    }

    // 정수형끼리의 연산이므로 소수점 이하는 버림된다.
    int middle = (start + end) / 2;

    if(arr[middle] == target)
    {
        return true;
    }

    if(arr[middle] < target)
    {
        return recursive_binary_search(target, middle + 1, end);
    }
    else
    {
        return recursive_binary_search(target, start, middle - 1);
    }
}

bool loop_binary_search(int target, int start, int end)
{
    int middle;
    while(start <= end)
    {
        middle = (start + end) / 2;

        if(arr[middle] == target)
        {
            return true;
        }

        if(arr[middle] > target)
        {
            end = middle - 1;
        }
        else
        {
            start = middle + 1;
        }
    }

    return false;
}

트리 자료구조

이진 탐색은 \(O(log(N))\) 이라는 매우 빠른 속도를 보여주지만 정렬된 배열 에서만 동작한다는 단점이 있습니다.
이 단점을 개선한 것이 트리 구조 를 이용한 이진 탐색 트리입니다.

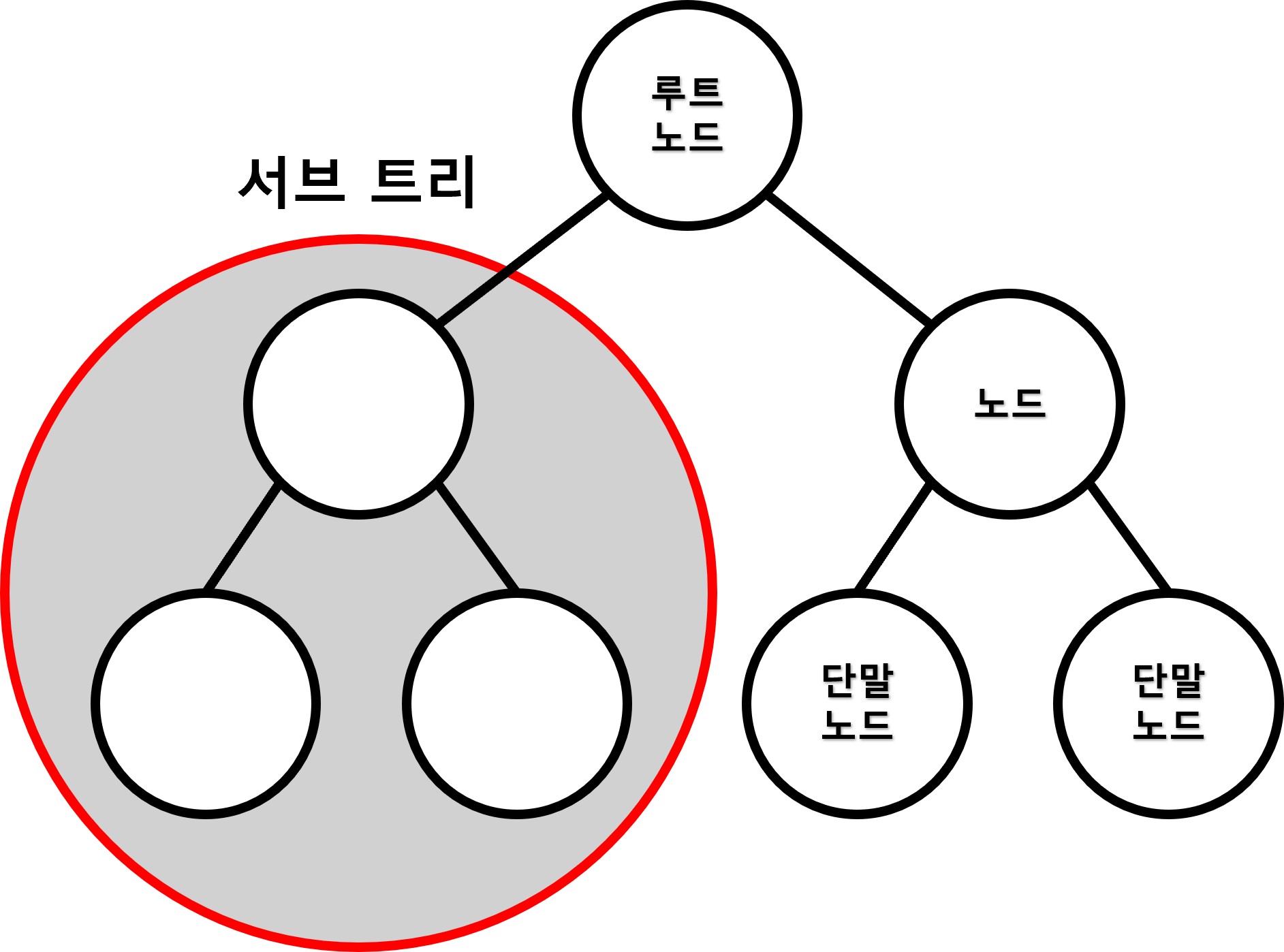
먼저 트리는 다음과 같은 규칙을 지켜 생성되는 자료구조입니다.

1. 트리는 부모 노드와 자식 노드 의 관계로 표현된다.
2. 트리의 최상단 노드를 루트 노드 라고 한다.
3. 트리의 최하단 노드를 단말 노드 라고 한다.
4. 트리에서 일부를 떼어내도 트리 구조이며 이를 서브 트리 라고 한다.
5. 트리는 계층적이고 정렬된 데이터 를 다루기 적합하다.

이진 탐색 트리

트리의 형태는 매우 다양한데 그 중 가장 간단한 형태가 이진 탐색 트리입니다.
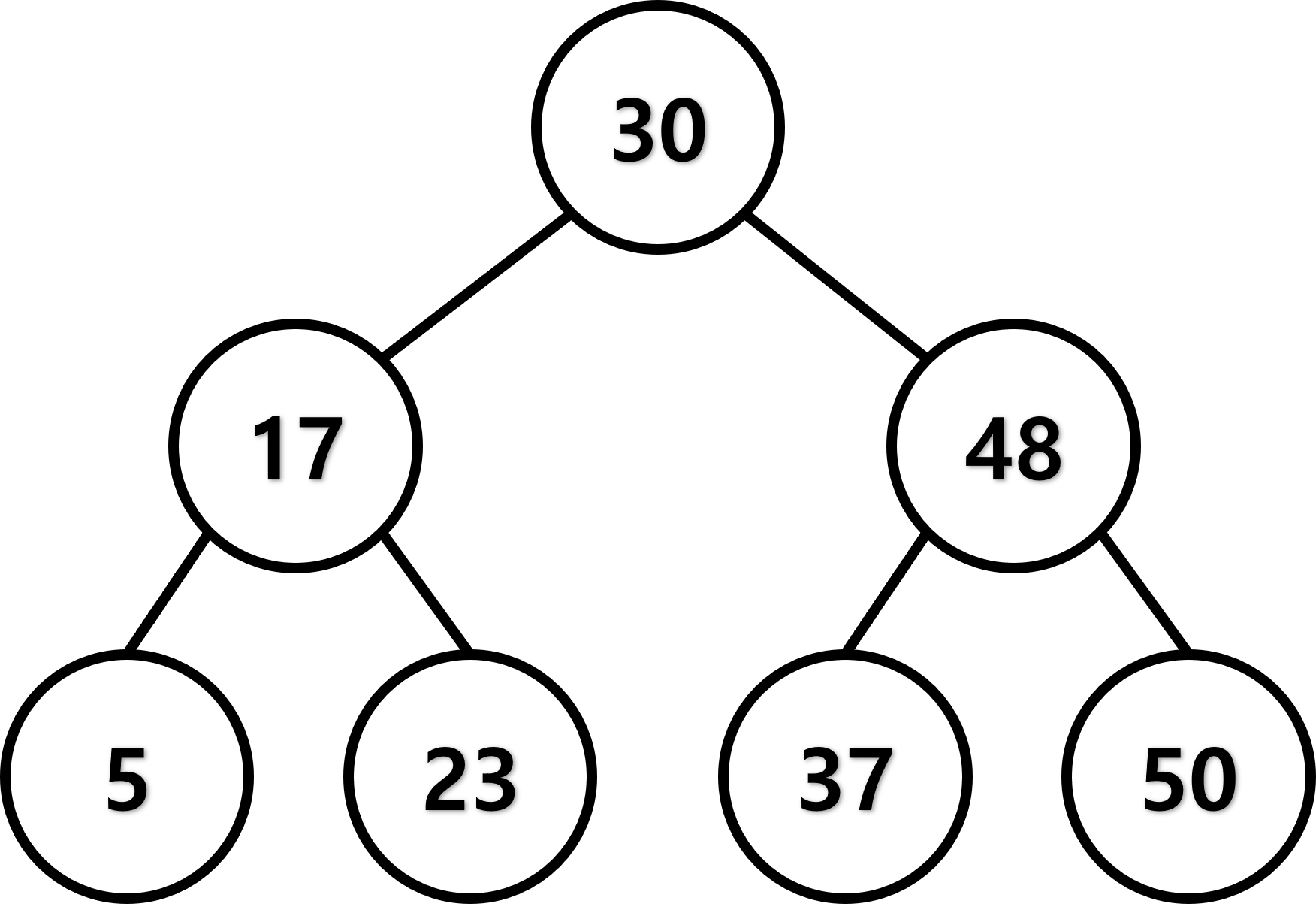
이진 탐색 트리는 위의 트리 자료구조의 기본 규칙을 지키며 추가로 2가지 규칙이 더 있습니다.

1. 부모 노드보다 왼쪽 자식 노드가 작다.
2. 부모 노드보다 오른쪽 자식 노드가 크다.

이 규칙에 맞춰 생성된 트리는 다음과 같습니다.