[자료구조] 균형 이진 탐색 트리 - AVL 트리
이진 트리의 약점
이전 포스트에서 이진 트리에 대해 설명했었습니다.
그리고 이진 트리의 약점으로 모든 노드가 1개의 자식만 갖게되어 일렬로 만들어진 트리가 있었습니다.
이 트리의 이름은 편향 이진 탐색 트리라고 부릅니다.
이러한 트리를 개선하고자 만들어진 자료 구조가 균형 이진 탐색 트리 입니다.
이진 트리가 균형 잡는 방법
균형 이진 탐색 트리의 핵심은 왼쪽 서브 트리와 오른쪽 서브 트리의 높이 차이가 1 이하 인 트리입니다.
균형 인수를 어느 정도로 두고 균형 잡는 방법을 어떻게 할지에 따라
AVL 트리, Red-Black 트리, Trie, 힙, B-트리, B+트리 등으로 나뉩니다.
이번 포스트에서는 AVL 트리에 대해서 살펴보겠습니다.
AVL 트리란?
AVL 트리는 왼쪽 서브 트리와 오른쪽 서브 트리의 높이 차가 1 이하 인 트리를 뜻합니다.
서브 트리 간 높이 차이 값을 균형 인수(Balance Factor)라고 합니다.
AVL 트리는 트리에서 삽입, 삭제가 일어났을 때, 트리 스스로 균형을 맞추기 위해 노드들을 재배치합니다.
균형이 맞춰진 트리이기 때문에 노드의 개수가 N 개 일 때 삽입, 삭제, 탐색 모두 \(O(log(N))\) 안에 가능합니다.
그러나 삽입, 삭제 연산이 빈번하게 발생할 경우, 매번 균형을 맞춰야 하기 때문에 속도가 저하될 수 있습니다.
균형 인수 (Balance Factor)
BF(node) = node 왼쪽 서브 트리 높이 - node 오른쪽 서브 트리 높이
AVL 트리에서 모든 노드는 균형 인수를 갖고 있습니다.
균형 인수는 위와 같은 공식으로 구할 수 있으며, -1, 0, 1 중 하나의 값만 갖을 수 있습니다.
만약 균형 인수가 -1, 0, 1 이 아니라면 그 트리는 균형이 깨진 트리로 이때, 균형을 맞추면 됩니다.
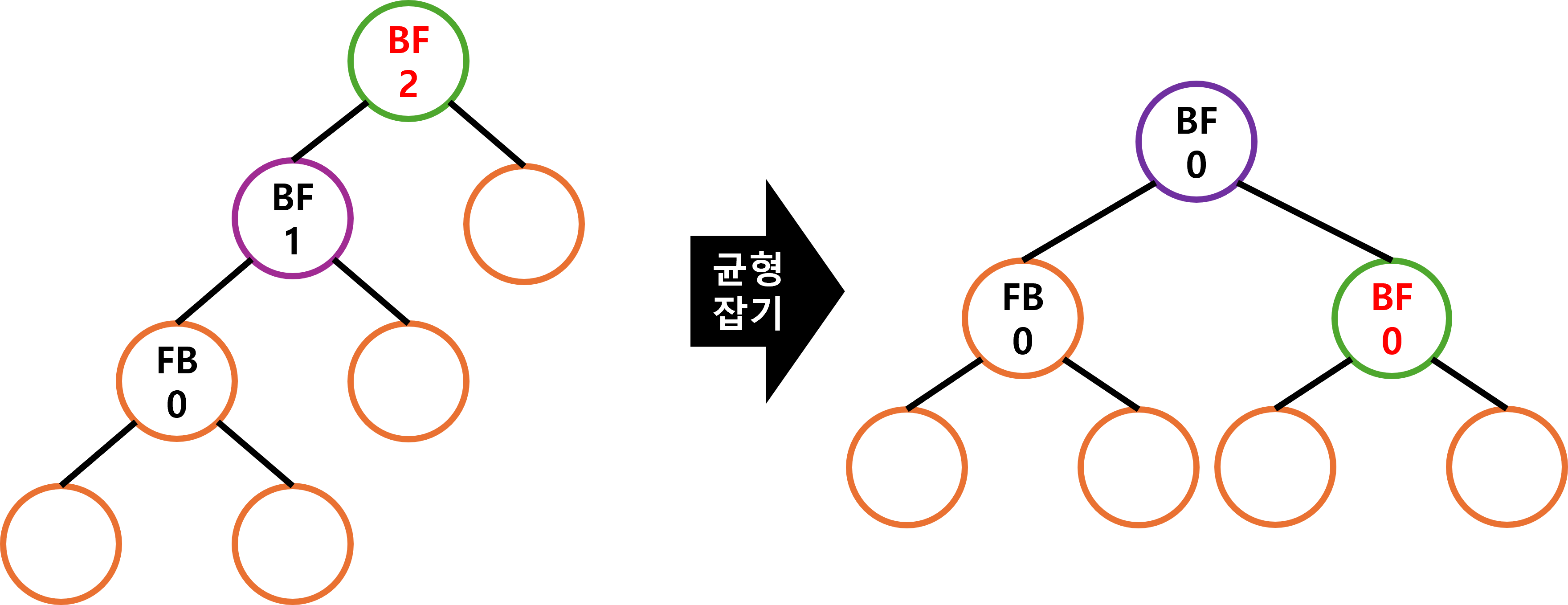
AVL 트리가 균형을 맞추는 방법으로 회전 을 사용하며 회전은 우회전, 좌회전 이 존재합니다.
우회전 (Right Rotatioin)
- 보라색 노드의 오른쪽 자식 노드 를 초록색 노드로 변경
- 초록색 노드의 왼쪽 자식 노드를 보라색 노드의 오른쪽 서브 트리 로 변경
AVL 트리의 우회전은 2개의 단계를 거쳐 진행됩니다.
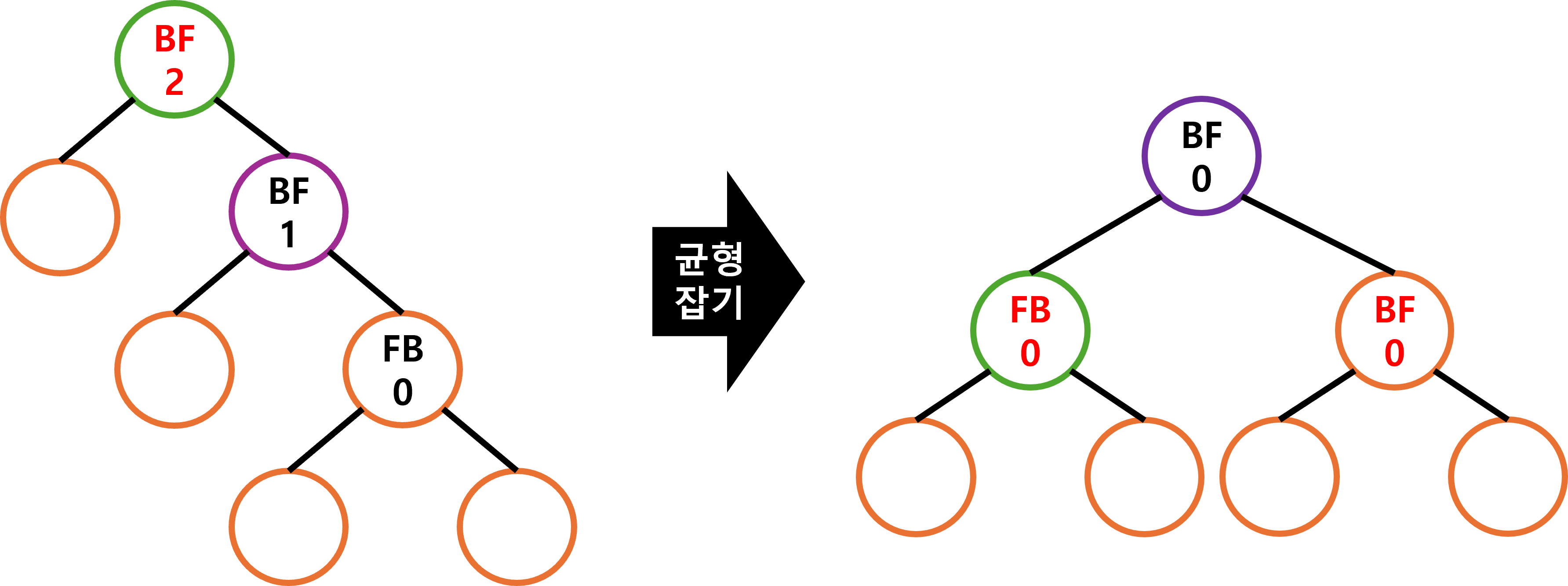
좌회전 (Left Rotation)
- 보라색 노드의 왼쪽 자식 노드 를 초록색 노드로 변경
- 초록색 노드의 오른쪽 자식 노드를 보라색 노드의 왼쪽 서브 트리 로 변경
AVL 트리의 우회전은 2개의 단계를 거쳐 진행됩니다.
AVL 트리 시뮬레이터
AVL 트리를 글만 읽고 완벽하게 이해하기란 어려울 수 있습니다.
따라서 AVL 시뮬레이터 사이트를 통해 직접 트리를 사용해 보면서
어떻게 동작하는지 살펴보는 것을 추천합니다.
개인 공부 기록용 블로그입니다. 틀린 부분이 있을 경우 댓글 혹은 메일로 지적해주시면 감사하겠습니다!