[백준][7579] 앱

이 포스트는 백준 사이트의 앱 문제 풀이입니다.

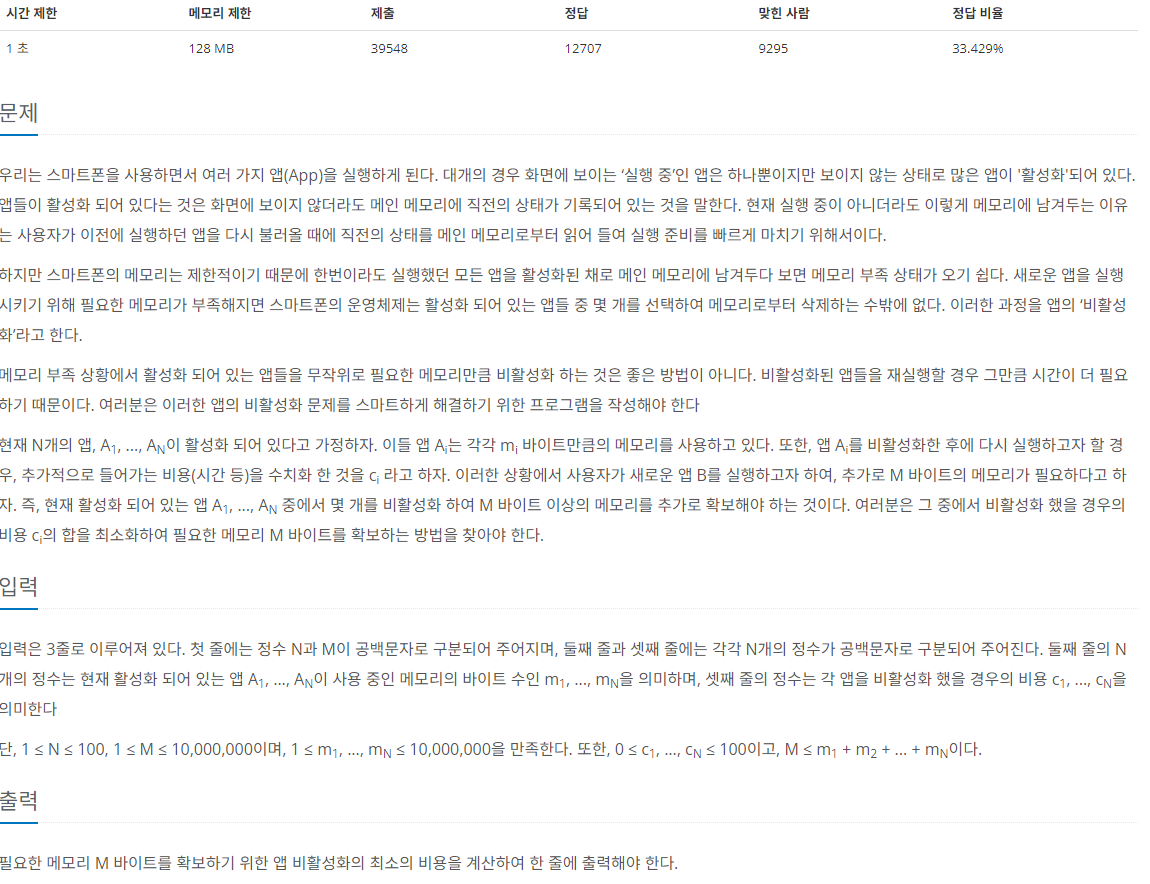
문제

해결 과정

이 문제는 DP 테이블을 활용하여 해결할 수 있는 문제입니다.

또 다른 대표 DP 문제인 배낭 문제와 유사하게 메모리 교체 비용의 최소값을 구해야 합니다.
차이점이 있다면 배낭 문제의 경우, 최댓값을 구하는 것이 목표였지만
이 문제에서는 최솟값을 구하는 것이 목표라는 점 입니다.

DP 테이블은 2차원 배열을 사용하였습니다.
예를들어, DP[i][j]은 1번부터 i번까지에서 j만큼의 비용을 의미합니다.

따라서 이 DP 테이블과 각 앱에 대한 비용이 저장되어 있는 reboot 배열을 사용하여
문제를 해결하였습니다.

코드 구현

#include <iostream>
#include <vector>
using namespace std;

int N, M;
long long sum = 0;
vector<int> memory{ 0, };
vector<int> reboot{ 0, };

int DP[101][10001];

void input();
void make_dp_table();

int main() {
    input();

    make_dp_table();

    for(int i = 0; i <= sum; ++i) {
        if(DP[N][i] >= M) {
            cout << i;
            break;
        }
    }
    return 0;
}

void input() {
    ios_base::sync_with_stdio(false);
    cin.tie(0);

    cin >> N >> M;

    for (int i = 0, cost; i < N; ++i) {
        cin >> cost;
        memory.push_back(cost);
    }

    for (int i = 0, cost; i < N; ++i) {
        cin >> cost;
        reboot.push_back(cost);
        sum += cost;
    }
}

void make_dp_table() {
    for(int i = 1; i <= N; ++i) {
        for(int j = 0; j <= sum; ++j) {
            if(j - reboot[i] >= 0) {
                DP[i][j] = max(DP[i][j], DP[i - 1][j - reboot[i]] + memory[i]);
            }

            DP[i][j] = max(DP[i][j], DP[i - 1][j]);
        }
    }
}

실행 결과