[백준][1149] RGB 거리

이 포스트는 백준 사이트의 RGB거리 문제 풀이입니다.

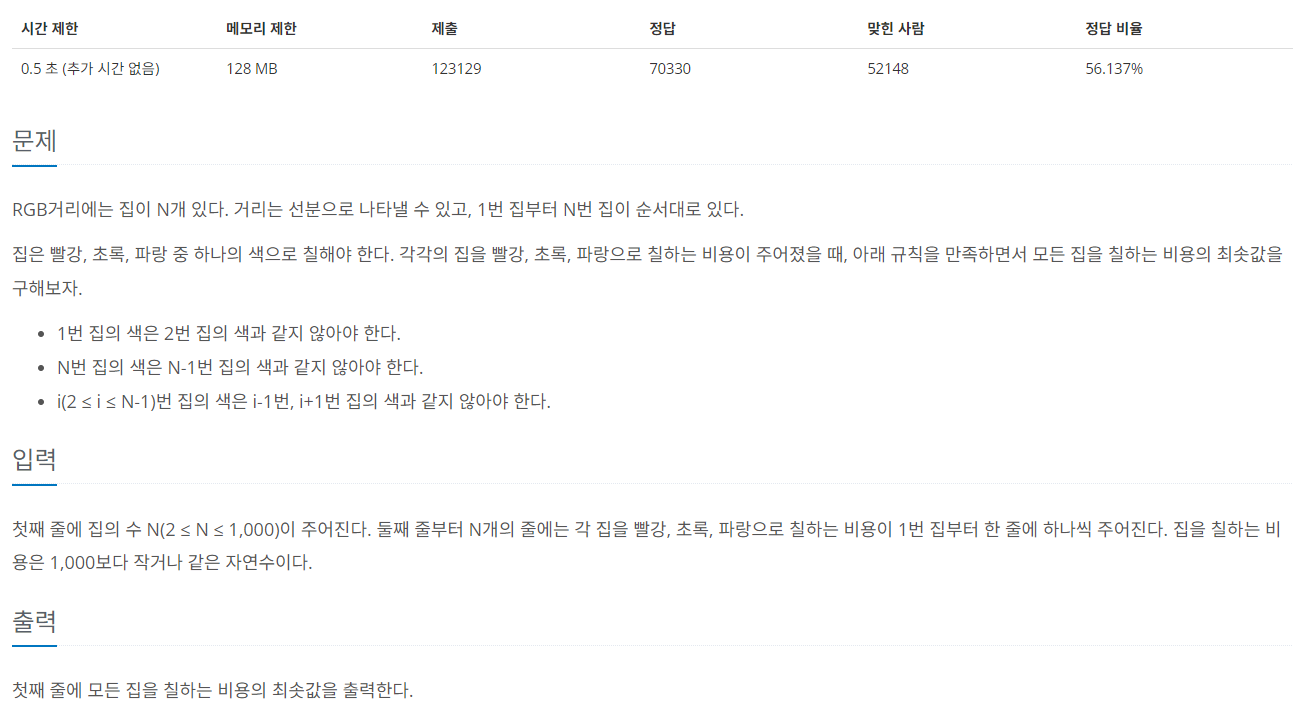
문제

해결 과정

문제를 작은 문제들로 나누어 풀 수 있는 문제로 DP(다이나믹 프로그래밍)를 활용하여 해결하였습니다.
문제에서 주어진 3가지 조건을 지키며 집을 칠하는 최소 비용을 구해야하므로
먼저, 점화식을 찾고자 하였습니다.

문제의 3가지 조건이 말하는 의미는 결국 이웃한 집끼리 색이 달라야 한다는 의미입니다.
i 번째 집을 빨간색으로 칠하면 i - 1 번째 집은 파랑 혹은 초록색 중 최소비용으로 칠해야 되는데
이때, i 번째 집에 대해 i - 1 번째 집과 i + 1 번째 집이 같아도 상관없으므로
i 번째 집의 색을 제외한 것 중 최소비용을 i + 1 칠하면 됩니다.

위 과정을 DP 테이블을 이용해 반복적으로 구하면 최소비용을 구할 수 있습니다.

코드 구현

#include <iostream>
using namespace std;

int main() {
	int N;
	cin >> N;
	int** RGB = new int*[N];
	for(int i = 0; i < N; ++i) {
		RGB[i] = new int[3];
		cin >> RGB[i][0] >> RGB[i][1] >> RGB[i][2];
	}
	
	int** DP = new int*[N];
	DP[0] = RGB[0];
	
	for(int i = 1; i < N; ++i) {
		DP[i] = new int[3];
		DP[i][0] = (DP[i - 1][1] > DP[i - 1][2] ? DP[i - 1][2] : DP[i - 1][1]) + RGB[i][0];
		DP[i][1] = (DP[i - 1][2] > DP[i - 1][0] ? DP[i - 1][0] : DP[i - 1][2]) + RGB[i][1];
		DP[i][2] = (DP[i - 1][0] > DP[i - 1][1] ? DP[i - 1][1] : DP[i - 1][0]) + RGB[i][2];
	}
	
	int min = (DP[N-1][0] < DP[N - 1][1] ? DP[N-1][0] : DP[N - 1][1]);
	min = (min > DP[N - 1][2] ? DP[N - 1][2] : min);
	cout << min;
	
	return 0;
}

실행 결과