[백준][10830] 행렬 제곱 (분할 정복 이용하기)

이 포스트는 백준 사이트의 행렬 제곱 문제 풀이입니다.

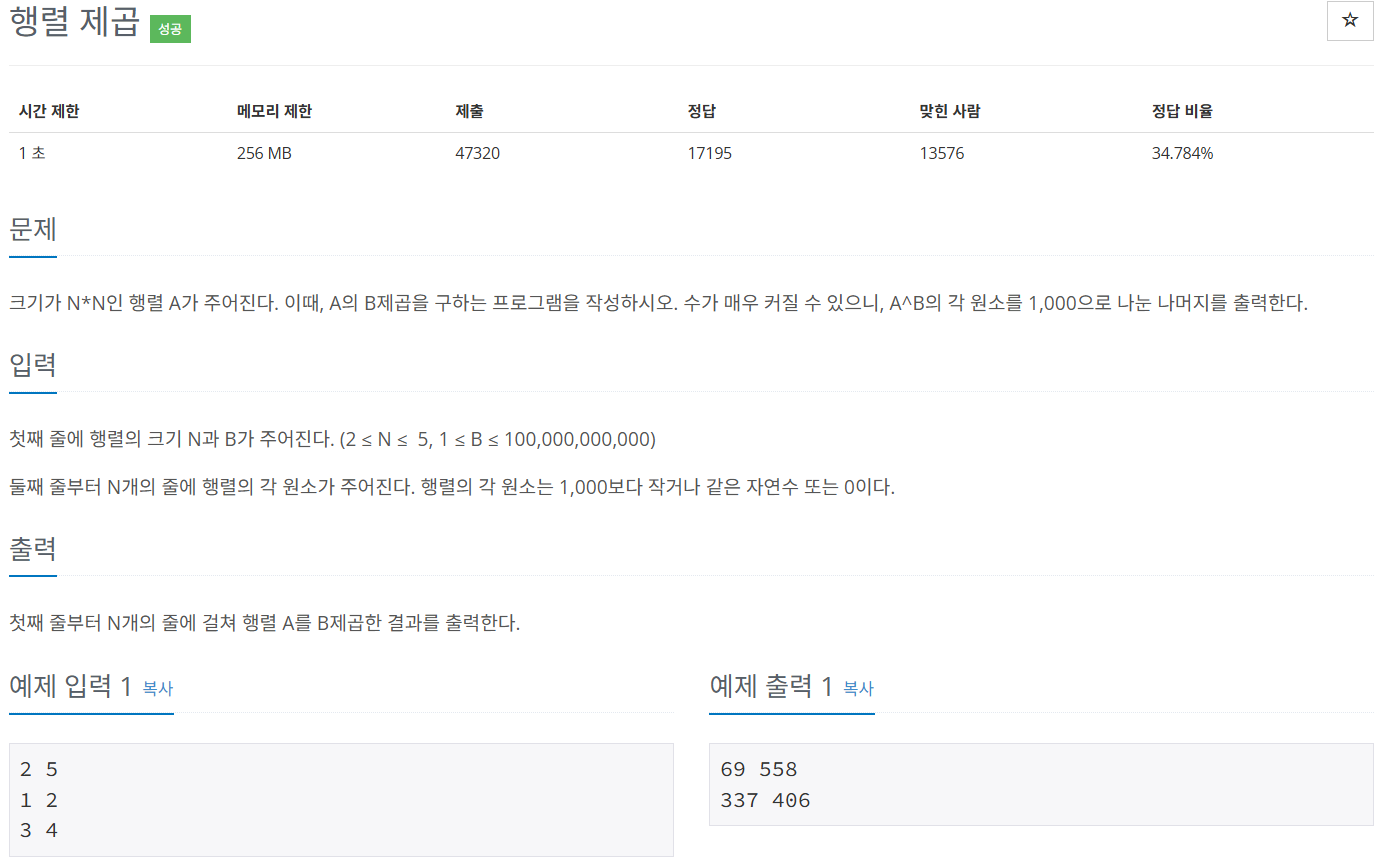
문제

해결 과정

문제의 요구 사항을 살펴보면 제곱 횟수(B의 값)이 최대 100,000,000,000번 (1’000억 번)이 될 수 있습니다.
행렬을 순차적으로 1’000억번 곱한다면 절대로 제한 시간 이내에 결과를 구할 수 없습니다.

따라서 이 문제는 순차 행렬 곱이 아닌 다른 방법을 사용해 문제를 해결해야 한다는 것을 알 수 있습니다.
문제에서 제공된 정보 중 주목해야할 것은 “한 개의 행렬을 제곱” 한다는 점입니다.
즉, 동일한 행렬이 반복적으로 곱해 결과를 도출할 수 있다는 특징이 있습니다.

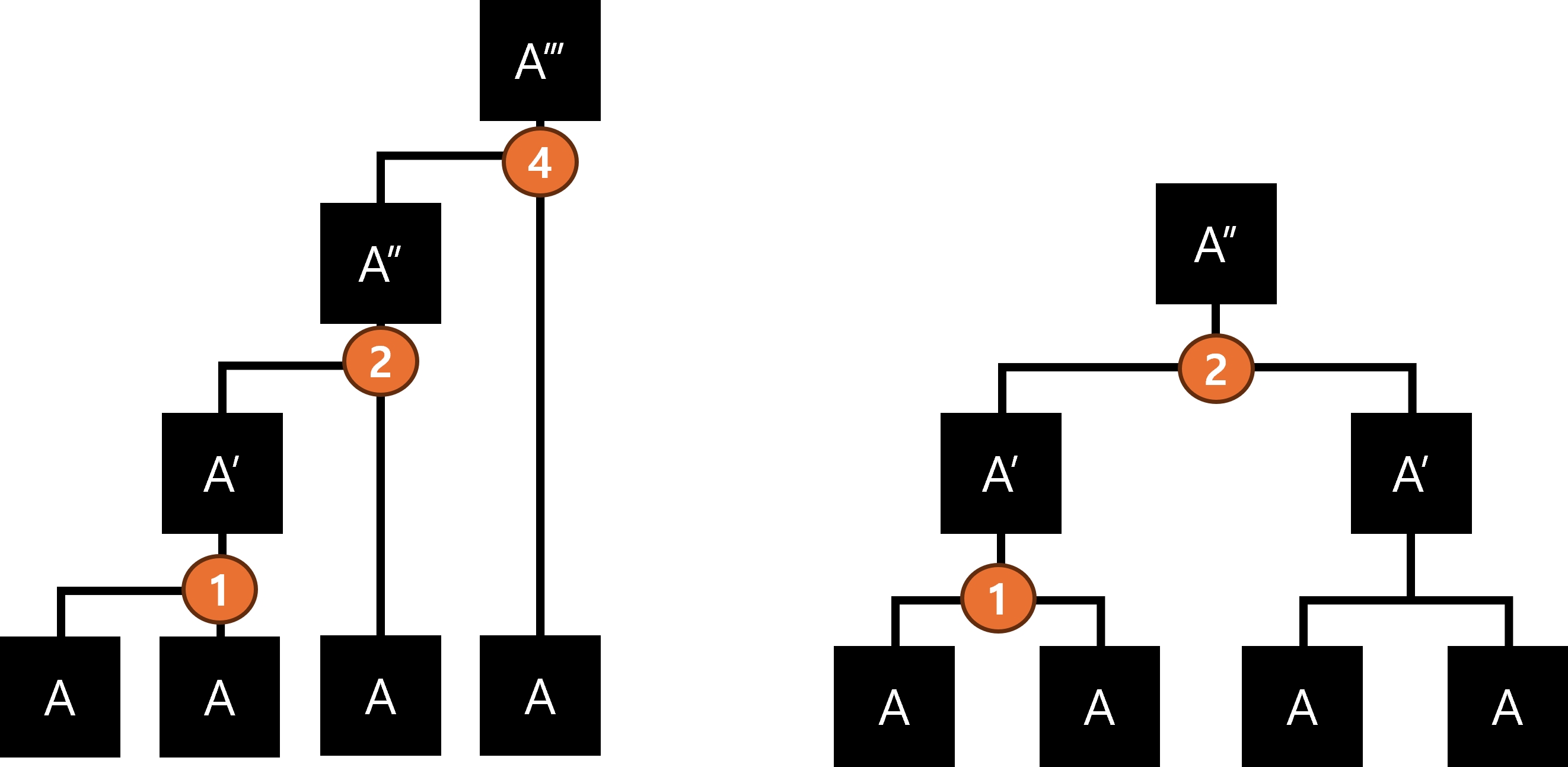
위 그림에서 왼쪽은 순차 곱셈을 이용한 연산의 과정을 표현한 것이고
오른쪽은 모든 행렬이 같다는 사실을 토대로 분할 정복을 사용해 연산하는 과정을 표현한 것 입니다.

번호가 적혀 있는 도형은 행렬의 곱셈이 수행되는 위치입니다.
위 그림에서는 행렬이 4개 뿐이라서 연산 횟수의 차이가 적지만, B의 최댓값으로 수행하게 된다면
연산 순서는 큰 차이가 날 것입니다.

코드로 구현하기 전 마지막으로 확인해야 할 점은 제곱 횟수가 홀수일 때 입니다.
홀수의 경우, 절반씩 줄여나가는 분할 정복에서 한번 더 연산이 필요합니다.
따라서 분할 정복을 수행하기 전 항상 남은 연산 수가 홀수인지 짝수인지 확인이 필요합니다.

위 내용을 토대로 코드를 작성하면 아래와 같습니다.

코드 구현

#include <iostream>
#include <vector>

#define MOD 1'000

using namespace std;

vector<vector<int>> multiply(const vector<vector<int>>& A, const vector<vector<int>>& B) {
    int n = A.size();
    vector<vector<int>> C(n, vector<int>(n, 0));
    for(int row = 0; row < n; ++row) {
        for(int col = 0; col < n; ++col) {
            for(int k = 0; k < n; ++k) {
                C[row][col] = (C[row][col] + A[row][k] * B[k][col]) % MOD;
            }
        }
    }
    return C;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    long long N, B;
    cin >> N >> B; 

    vector<vector<int>> matrix(N, vector<int>(N));
    for(int row = 0; row < N; ++row) {
        for(int col = 0; col < N; ++col) {
            cin >> matrix[row][col];
        }
    }

    vector<vector<int>> result(N, vector<int>(N, 0));
    for(int i = 0; i < N; ++i) result[i][i] = 1;
    while(B > 0) {
        if(B % 2 == 1) {
            result = multiply(result, matrix);   
        }
        
        matrix = multiply(matrix, matrix);
        B = B / 2;
    }

    for(int row = 0; row < N; ++row) {
        for(int col = 0; col < N; ++col) {
            printf("%d ", result[row][col]);
        }   printf("\n");
    }

    return 0;
}

실행 결과