[알고리즘] 세그먼트 트리 (Segment Tree)

세그먼트 트리는 연속된 데이터에서 특정 범위에 대한 합과 같은 연산이 필요할 때 사용되는 알고리즘 입니다.

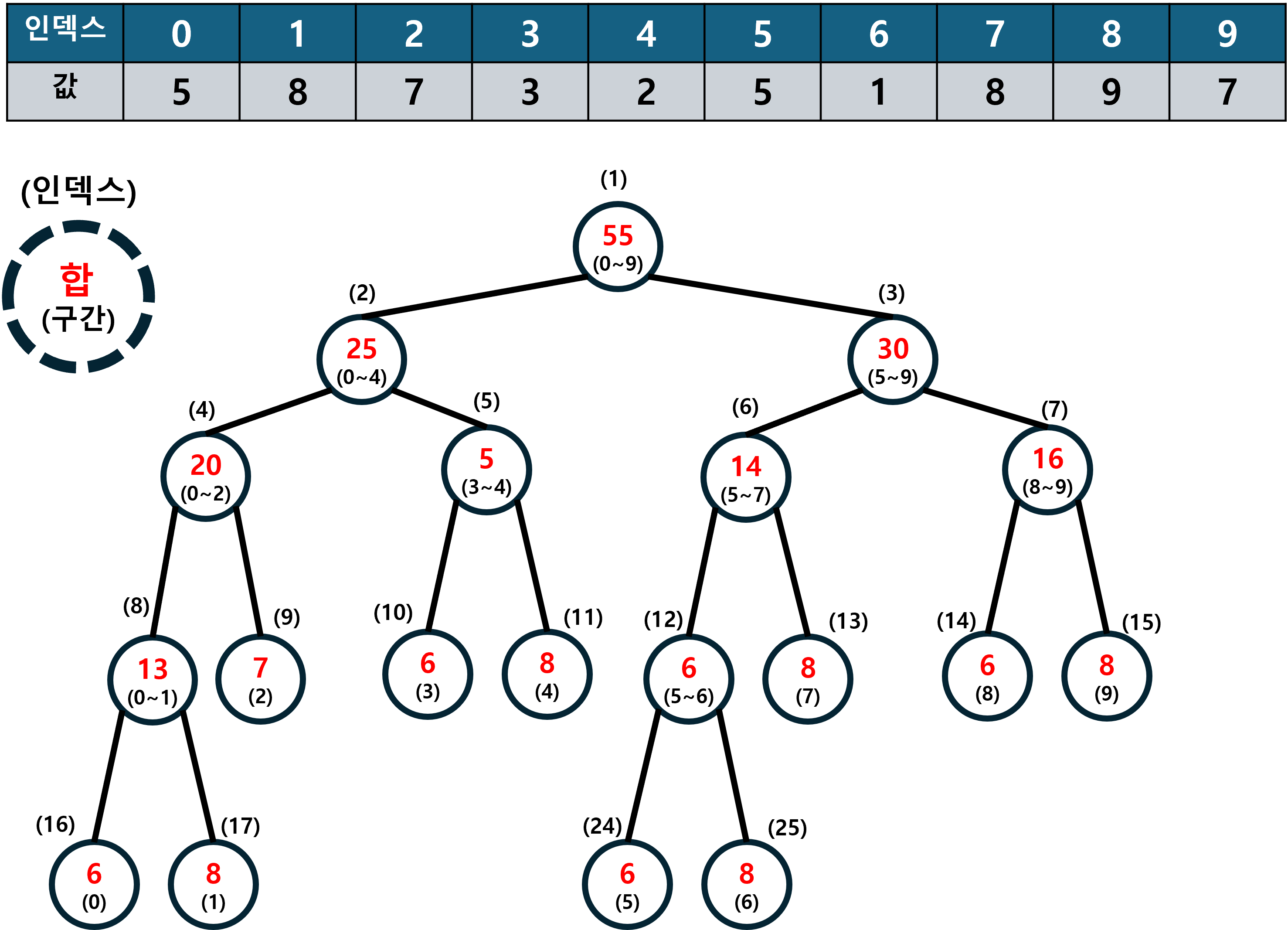
예를들어, {5, 8, 7, 3, 2, 5, 1, 8, 9, 7}이라는 배열에서
특정 범위인 (0번부터 시작할 때) 1번부터 9번까지 합을 빠르게 구하려고 합니다.

단순하게 연산한다면 반복문을 통해 순차적으로 방문하여 합을 계산할 수 있습니다.

int sum = 0;
for(int i = 1; i <= 9; ++i) {
    sum += arr[i];
}
cout << sum;

그러나 이러한 코드는 순차 탐색이기 때문에 숫자의 수가 N 개라면
시간 복잡도는 O(N)이 될 수 있습니다.
이 시간 복잡도를 개선할 수 있는 것이 트리 구조를 사용한 세그먼트 트리 입니다.

세그먼트 트리의 개념

세그먼트 트리는 이름처럼 트리를 활용하기 때문에 숫자의 개수가 N 개라고 하여도
시간 복잡도는 O(log(N))이 될 수 있습니다.

구간 합을 구하기 위한 세그먼트 트리의 특징은 아래와 같습니다.

• 트리의 형태는 이진 트리
• 루트 노드의 인덱스는 반드시 1부터 시작
• 각 노드에는 고유의 번호가 존재
• 노드가 갖고 있는 정보는 특정 구간과 그 구간의 합

위 특징들을 고려하여 세그먼트 트리를 그리면 아래와 같습니다.

이 트리에서 루트 노드의 인덱스를 1로 둔 것은 탐색을 빠르게 진행하기 위해서 입니다.
현재 노드의 인덱스에서 자식 노드로 넘어갈 때,
인덱스의 숫자는 왼쪽 자식일 경우 \((index) \times 2\)이고,
오른쪽 자식 노드일 경우 \((index) \times 2 + 1\)이 됩니다.

만약 루트 노드의 인덱스가 0일 경우, 이러한 탐색 자체가 불가능합니다.

\((0 \times 2) = 0\)이기 때문에 불가능

세그먼트 트리 구현하기

세그먼트 트리는 재귀적으로 구현하면 코드를 간단하게 작성할 수 있습니다.
이때, 다이나믹 프로그래밍이 지금의 문제를 작은 문제들로 나누는 것처럼
현재의 노드가 자식 노드들의 합이라는 규칙을 활용할 수 있습니다.

number라는 배열에 각 숫자가 있고, tree라는 배열에 구간합을 저장하면
세그먼트 트리를 재귀적으로 생성하는 코드는 아래와 같습니다.

int init_segment_tree(int start, int end, int node) {
    if(start == end) {
        return tree[node] = number[start];
    }

    int mid = (start + end) / 2;
    return tree[node]
        = init_segment_tree(start, mid, node * 2) // 왼쪽 자식 트리이므로 x 2
        + init_segment_tree(mid + 1, end, node * 2 + 1); // 오른쪽 자식 트리이므로 x 2 + 1
}

여기서 중요한 것은 인덱스의 번호가 완전 이진 트리의 노드 개수와 같다는 것 입니다.
따라서 모든 공간을 사용하지는 않지만, 노드의 인덱스 번호로 활요하기 위해
숫자의 개수가 N이라면 \(N \times 4\) 만큼의 공간이 필요합니다.