[알고리즘] A* 알고리즘 구현해보기
개인 학습을 기록한 내용을 담고 있어 추후 수정될 수 있습입니다.
A* 알고리즘이란
A* 알고리즘은 최단 경로 탐색 알고리즘 중 하나로 유명합니다.
주어진 지도(map)에서 출발 지점부터 도착 지점까지 최적의 경로를 찾는 기술입니다.
A* 코드의 구조가 다익스트라 최단거리 알고리즘과 닮았다는 특징이 있지만
다익스트라의 경우, 우선순위 큐와 거리 배열로 최단 거리를 구하지만
A* 알고리즘은 우선순위 큐와 휴리스틱(Huristic) 거리 측정값을 활용해서 최단거리를 구하는 알고리즘입니다.
A* 알고리즘 동작 순서
A* 알고리즘 동작의 핵심은 휴리스틱 값과 현재까지 이동거리 값입니다.
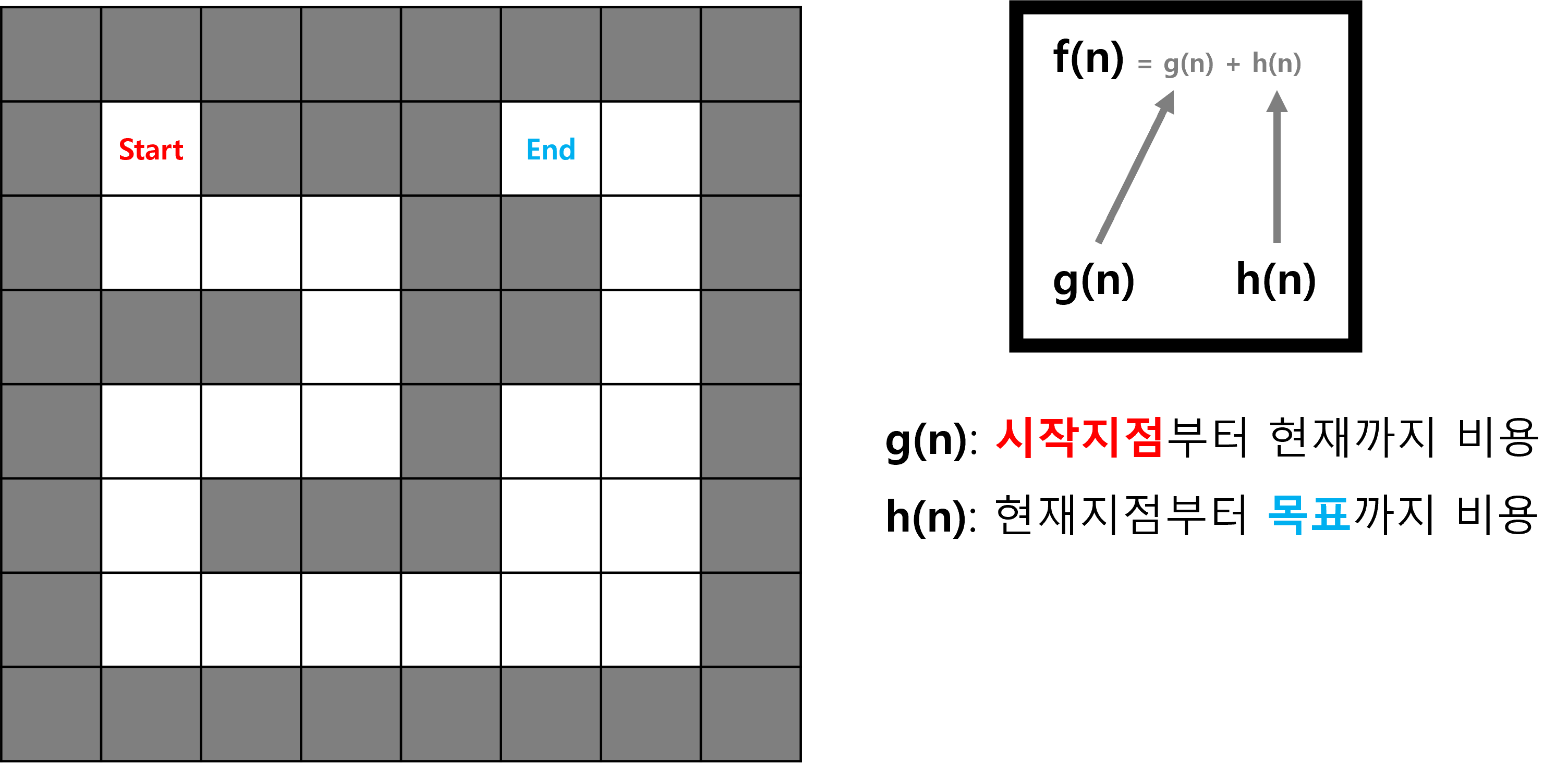
위의 그림은 8 x 8 지도에서 회색은 장애물, 흰색은 이동 가능한 칸 입니다.
그리고 g(n)함수의 값은 시작지점부터 현재지점까지의 거리값이고
h(n)함수의 값은 현재지점부터 목표지점까지의 거리값을 의미합니다.
이 포스트에서는 휴리스틱 거리 계산으로 널리 사용되는 맨해튼 거리 측정법을 사용하겠습니다.
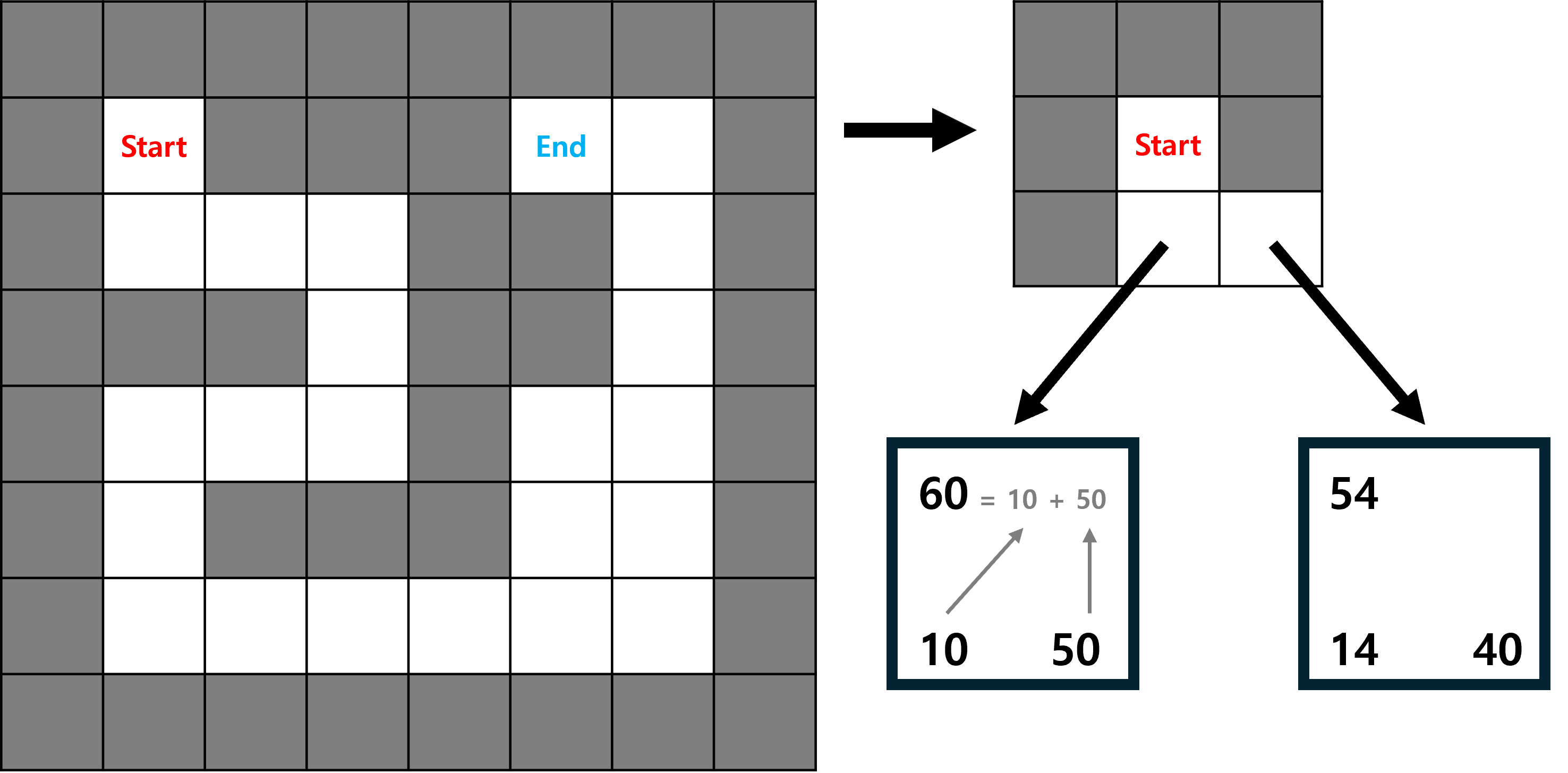
현재 위치(Start지점)에서 이동가능한 칸은 그림처럼 2개가 있습니다.
먼저, 바로 아래 칸의 g(n)과 h(n)을 구해보겠습니다.
이 지도에서 상하좌우를 한 칸 이동하는 거리는 10, 대각선으로 이동하는 값을 14라고 하겠습니다.
\(\sqrt{10^2 + 10^2} = 14.14...\) 이므로 대각선 거리는 14라고 하겠습니다.
g(n)의 값은 아래쪽으로 한 칸 이동했으므로 10,
h(n)의 값은 아래 칸에서 ‘goal’칸 까지 장애물을 무시한 맨해튼 거리인 50 입니다.
따라서 총 비용 값은 60(10 + 50)입니다.
우측 하단 대각선에 있는 칸의
g(n)값은 대각선으로 한 칸 이동했으므로 14,
h(n)값은 ‘goal’칸 까지 장애물을 무시한 맨해튼 거리인 40 입니다.
따라서 총 비용 값은 54(14 + 40)입니다.
두 칸을 비교했을 때, 대각선으로 이동하는 값이 더 작으므로(54 < 60) 대각선으로 이동합니다.
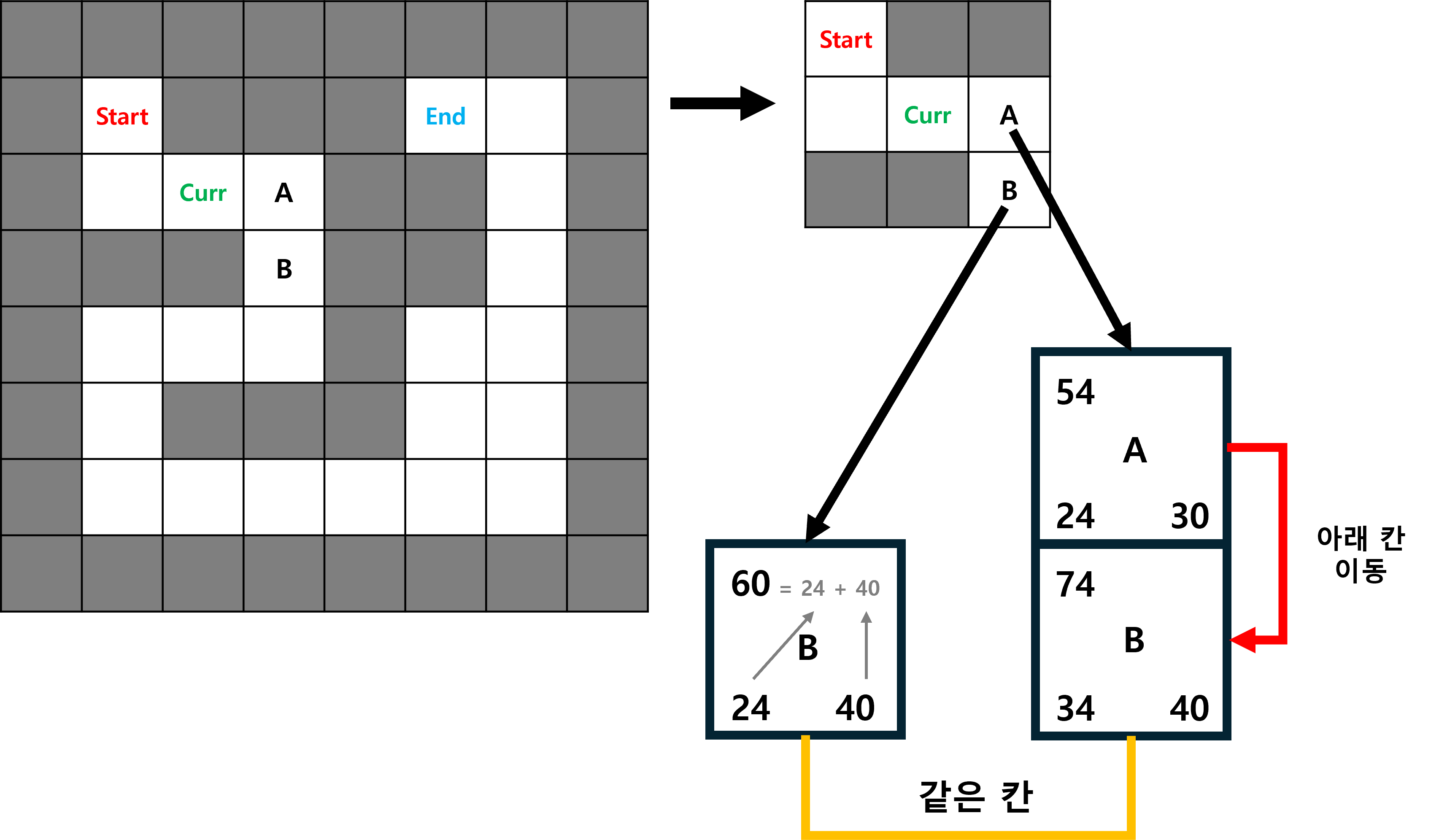
위의 과정에 따라 현재 위치를 ‘Start’에서 ‘Curr’로 이동하였습니다.
이번에도 위의 과정처럼 g(n)과 h(n)값을 구하여
오른쪽 칸으로 이동할지, 아래쪽 대각선으로 이동할지를 결정합니다.
이때, 이전 과정과 차이점은 새로운 g(n)값에 이전 g(n)값이 더해진다는 것입니다.
오른쪽 칸으로 이동한다면 다음에는 반드시 아래 칸으로 이동해야 하는데
이는 대각선으로 이동한 g(n)값보다 크기 때문에
결국 이 과정에서도 대각선으로 이동하게 됩니다.
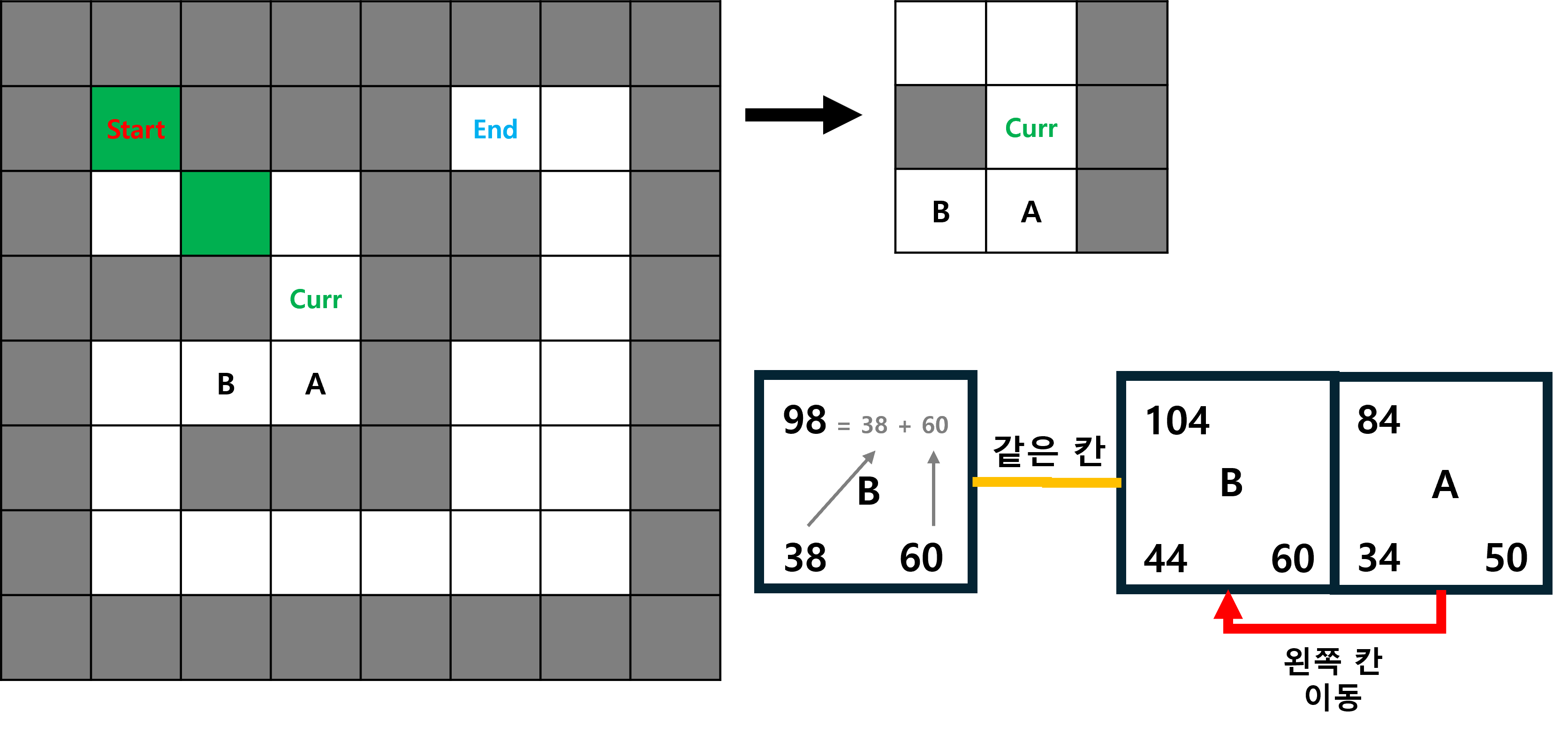
위의 두 과정처럼 각 칸의 g(n), h(n)값을 비교하면서 이동하면 목표까지의 최단거리를 구할 수 있습니다.
A* 에서는 2가지 컨테이너가 사용되는데,
첫 번째는 위 과정에서 사용할 우선순위 큐인 open_q,
두 번째로 바로 위 그림처럼 지금까지의 과정으로 확인된 최단거리(초록색 칸)을 담을 close_q 가 있습니다.
전체 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
#include <iostream>
#include <vector>
#include <queue>
#include <map>
#include <cmath>
#include <algorithm>
#define BOARD_SIZE 20
using namespace std;
struct POINT {
int x, y;
POINT& operator=(const POINT& rhs) {
this->x = rhs.x;
this->y = rhs.y;
return *this;
}
};
bool operator<(const POINT& lhs, const POINT& rhs) {
if (lhs.x == rhs.x)
return lhs.y < rhs.y;
return lhs.x < rhs.x;
}
struct Node {
POINT curr_location;
POINT prev_location;
Node& operator=(const Node& rhs) {
this->curr_location = rhs.curr_location;
this->prev_location = rhs.prev_location;
return *this;
}
};
bool operator<(const Node& lhs, const Node& rhs) {
return false;
}
struct Huristic {
int move_dist;
float pre_diction_dist;
};
bool operator<(const Huristic& lhs, const Huristic& rhs) {
return (lhs.move_dist + lhs.pre_diction_dist)
< (rhs.move_dist + rhs.pre_diction_dist);
}
vector<vector<int>> board;
vector<POINT> AStar(POINT start, POINT goal) {
priority_queue<pair<Huristic, Node>,
vector<pair<Huristic, Node>>,
greater<pair<Huristic, Node>>> open_q;
map<POINT, POINT> close_q;
pair<Huristic, Node> start_point;
start_point.second.curr_location = start;
start_point.second.prev_location = POINT{ -1, -1 };
start_point.first.move_dist = 0;
start_point.first.pre_diction_dist = -1;
open_q.push(start_point);
int dir_y[8]{ 1, 1, 0, -1, -1, -1, 0, 1 };
int dir_x[8]{ 0, 1, 1, 1, 0, -1, -1, -1 };
while (false == open_q.empty()) {
Node curr_node = open_q.top().second;
Huristic curr_huristic = open_q.top().first;
open_q.pop();
if (close_q.find(curr_node.curr_location) != close_q.end())
continue;
close_q.insert(make_pair(curr_node.curr_location, curr_node.prev_location));
int x = curr_node.curr_location.x;
int y = curr_node.curr_location.y;
if (x == goal.x && y == goal.y)
break;
for (int dir = 0; dir < 8; ++dir) {
int new_x = x + dir_x[dir];
int new_y = y + dir_y[dir];
if (new_x < 0 || new_x >= BOARD_SIZE || new_y < 0 || new_y >= BOARD_SIZE)
continue;
if (1 == board[new_y][new_x])
continue;
if (close_q.find(POINT{ new_x, new_y }) != close_q.end())
continue;
Huristic huristic;
Node next_node{};
int delta_x = new_x - goal.x;
int delta_y = new_y - goal.y;
float direct_dist = sqrt(pow(delta_x, 2) + pow(delta_y, 2));
huristic.move_dist = curr_huristic.move_dist + 1;
huristic.pre_diction_dist = direct_dist;
next_node.curr_location = POINT{ new_x, new_y };
next_node.prev_location = POINT{ x, y };
open_q.push(make_pair(huristic, next_node));
}
}
vector<POINT> result_path;
if (close_q.find(goal) != close_q.end()) {
POINT location = goal;
while (location.x != -1) {
result_path.push_back(location);
location = close_q[location];
}
}
reverse(result_path.begin(), result_path.end());
return result_path;
}
int main() {
board = vector<vector<int>>{
{1, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 1, 1, 1, 0, 0, 1},
{1, 0, 0, 0, 1, 1, 0, 1},
{1, 1, 1, 0, 1, 1, 0, 1},
{1, 0, 0, 0, 1, 0, 0, 1},
{1, 0, 1, 1, 1, 0, 0, 1},
{1, 0, 0, 0, 0, 0, 0, 1},
{1, 1, 1, 1, 1, 1, 1, 1}
};
auto path = AStar(POINT{ 1, 1 }, POINT{ 5, 1 });
if (false == path.empty()) {
for (auto p : path) {
board[p.y][p.x] = 2;
}
}
else {
printf("Path is empty\n");
}
for (auto line : board) {
for (int c : line) {
if (c == 2) {
printf("O ");
}
else if (c == 1) {
printf("X ");
}
else {
printf(" ");
}
}
printf("\n");
}
return 0;
}